《2025年全品学练考八年级数学上册苏科版江苏专版》

尝试 如图1-3-5,补充条件使下列各题能根据“SAS”证明△ABC≌△BAD.

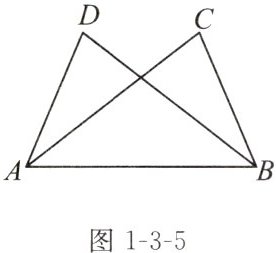
(1)已知AD= BC,再添加∠DAB= ∠CBA即可;
(2)已知∠DBA= ∠CAB,再添加BD= AC即可.

答案：
(1)DAB CBA
(2)BD AC

例1(教材典题)如图1-3-6,A,B分别是线段OD,OC上的点,OC= OD,OA= OB.求证:△OAC≌△OBD.

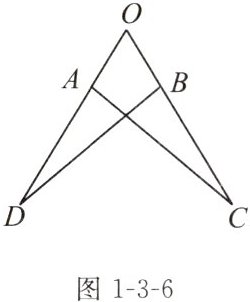
讨论 图1-3-6所示的图形是轴对称图形吗?如果是,你能画出对称轴吗?

答案： 证明:在△OAC和△OBD中,OA=OB,∠AOC=∠BOD,OC=OD,
∴△OAC≌△OBD(SAS). 是轴对称图形,画出对称轴略

例2(教材典题)如图1-3-7,AB= AC,AD= AE,∠1= ∠2.
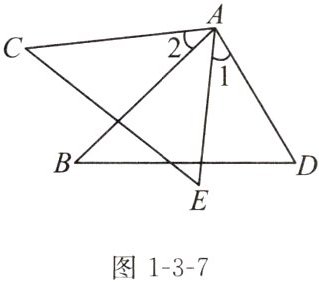
求证:△ABD≌△ACE.

答案： 证明:
∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE(等式的性质),即∠BAD=∠CAE.在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).

探究 我们知道,两边及夹角分别相等的两个三角形全等.那么,两边及其中一边所对角分别相等的两个三角形全等吗?

答案： 不一定全等.例:如图,在△ABC和△ABD中,AB=AB,∠B=∠B,AC=AD,显然△ABC和△ABD不全等

学方法
根据“SAS”添加判定两个三角形全等的条件
(1)如果已知两边对应相等,需添加两边所夹的角相等;
(2)如果已知一边一邻角对应相等,需添加夹该角的另一边相等.
学方法
证明三角形全等时要关注三类条件:第一类是直接条件,给出全等三角形的对应边、对应角,可以直接运用;第二类是隐含条件,例如公共边、公共角、对顶角等,无需证明,直接得到;第三类是间接条件,可以根据相关知识将其转化为直接条件.

答案：
(1)两边所夹的角相等
(2)夹该角的另一边相等 公共边 公共角 对顶角

反思
用SAS证明三角形全等,如果具备一边一邻角条件时,还差什么条件?

答案： 还差夹这个角的另一边.