《2025年全品学练考八年级数学上册苏科版江苏专版》

活动探究
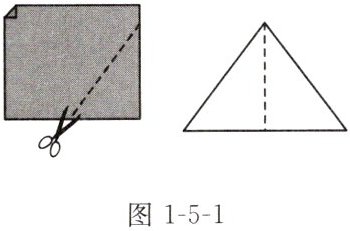
如图 1 - 5 - 1,把一张长方形纸片对折,沿虚线剪下并展开,得到的三角形有什么特征？

答案： 解:这个三角形有两条边相等,有两个角相等.

如图 1 - 5 - 2,在等腰三角形 ABC 中,AB = AC。
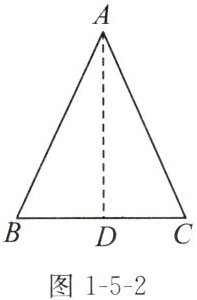
作边 BC 的中线 AD。在△ABD 和△ACD 中,AB = AC,BD = CD,AD = AD,通过“SSS”,可以证明△ABD ≌ △ACD,所以∠B = ∠C。

答案： CD SSS C

例 1(教材典题)如图 1 - 5 - 3,在△ABC 中,AB = AC,点 D 在 BC 上,且 AD = BD。
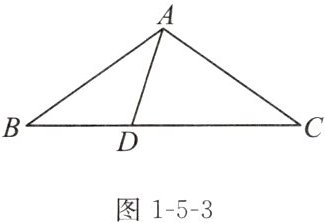
求证：∠ADB = ∠BAC。

答案： 【解析】：本题可根据等腰三角形的性质，找出与$\angle ADB$和$\angle BAC$相关的角，通过等量代换来证明$\angle ADB = \angle BAC$。
已知$AB = AC$，根据等腰三角形的性质：等腰三角形两底角相等，可得$\angle B = \angle C$。
又因为$AD = BD$，同样根据等腰三角形两底角相等，可得$\angle B = \angle BAD$。
在$\triangle ABC$中，根据三角形内角和定理：三角形内角和为$180^{\circ}$，则$\angle BAC + \angle B + \angle C = 180^{\circ}$，即$\angle BAC=180^{\circ}-2\angle B$。
在$\triangle ABD$中，$\angle ADB + \angle B + \angle BAD = 180^{\circ}$，因为$\angle B = \angle BAD$，所以$\angle ADB = 180^{\circ}-2\angle B$。
由此可得$\angle ADB = \angle BAC$。
【答案】：证明：
∵$AB = AC$，
∴$\angle B = \angle C$（等边对等角）。
∵$AD = BD$，
∴$\angle B = \angle BAD$（等边对等角）。
在$\triangle ABC$中，$\angle BAC + \angle B + \angle C = 180^{\circ}$，
∴$\angle BAC = 180^{\circ}-2\angle B$。
在$\triangle ABD$中，$\angle ADB + \angle B + \angle BAD = 180^{\circ}$，
∵$\angle B = \angle BAD$，
∴$\angle ADB = 180^{\circ}-2\angle B$。
∴$\angle ADB = \angle BAC$。

变式 如图 1 - 5 - 4,△ABC 中,∠A = 36°,点 D 在边 AC 上,AD = BD = BC,求∠DBC 的度数。

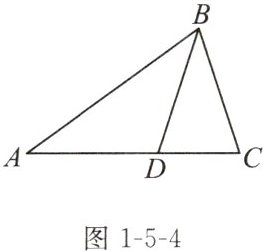
答案： 36°