《2025年全品学练考八年级数学上册苏科版江苏专版》

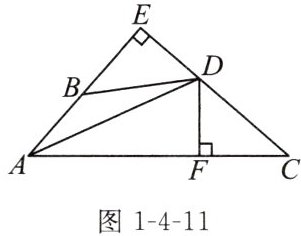
变式 如图1-4-11,已知AD平分∠BAC,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,且BE= CF,试判断BD和CD的数量关系,并说明理由.

答案： BD=CD 理由略

问题探究
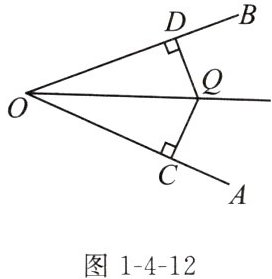
如果一个点到一个角的两边的距离相等,那么这个点在这个角的平分线上吗？如何证明？
证明：如图1-4-12,点Q在∠AOB内,QC⊥OA,QD⊥OB,垂足分别为C,D,且QC= QD.
画射线OQ,在△OCQ和△ODQ中,∠QCO= ∠QDO= 90°,OQ= OQ,QC= QD,
通过“HL”,可以证明Rt△OCQ≌Rt△ODQ,所以∠AOQ= ∠BOQ,所以点Q在∠AOB的平分线上.

答案： QDO 90 QD HL BOQ

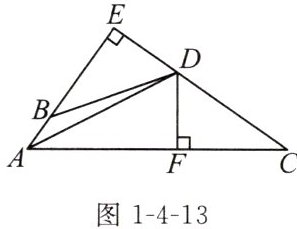
例2 如图1-4-13,BE= CF,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,且DB= DC.求证：AD平分∠BAC.

答案： 【解析】：本题可根据已知条件，通过证明三角形全等，得出对应角相等，再结合角平分线的判定定理来证明$AD$平分$\angle BAC$。
首先，由$DE\perp AB$，$DF\perp AC$，根据垂直的定义可知$\angle BED = \angle CFD = 90^{\circ}$。
已知$BE = CF$，$DB = DC$，在$\triangle BDE$和$\triangle CDF$中，根据“斜边直角边定理（$HL$）”可证明这两个直角三角形全等。
因为$\triangle BDE\cong\triangle CDF$，所以对应边$DE = DF$。
最后，根据角平分线的判定定理：到角两边距离相等的点在这个角的平分线上，由于$DE\perp AB$，$DF\perp AC$且$DE = DF$，所以点$D$在$\angle BAC$的平分线上，即$AD$平分$\angle BAC$。
【答案】：
证明：
∵$DE\perp AB$，$DF\perp AC$，
∴$\angle BED = \angle CFD = 90^{\circ}$。
在$Rt\triangle BDE$和$Rt\triangle CDF$中，
$\begin{cases}BE = CF \\DB = DC\end{cases}$
∴$Rt\triangle BDE\cong Rt\triangle CDF(HL)$。
∴$DE = DF$。
∵$DE\perp AB$，$DF\perp AC$，
∴点$D$在$\angle BAC$的平分线上，
即$AD$平分$\angle BAC$。