《2025年全品学练考八年级数学上册苏科版江苏专版》

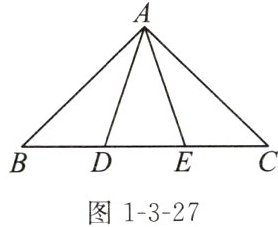
练习 如图1-3-27,在△ABC中,AB= AC,D,E是边BC的三等分点,AD= AE。求证：△ABD≌△ACE。

答案： 证明:
∵D,E 是边 BC 的三等分点,
∴BD=CE.
在△ABD 和△ACE 中,{AB=AC,
BD=CE,
AD=AE,
∴△ABD≌△ACE(SSS).

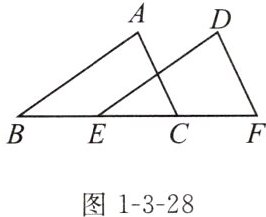
例2 (教材典题)已知：如图1-3-28,AB= DE,AC= DF,BE= CF。
求证：△ABC≌△DEF。

答案： 证明:
∵BE=CF,
∴BE+EC=CF+EC,即 BC=EF.
在△ABC 和△DEF 中,{AB=DE,
BC=EF,
AC=DF,
∴△ABC≌△DEF(SSS).

练习 已知：如图1-3-29,点A,C,F,D在同一直线上,AF= DC,AB= DE,BC= EF。求证：△ABC≌△DEF。

答案： 证明:
∵AF=DC,
∴AF-CF=DC-CF,即 AC=DF.
在△ABC 和△DEF 中,{AC=DF,
AB=DE,
BC=EF,
∴△ABC≌△DEF(SSS).

讨论 用三根细木棒钉成一个三角形框架,它的形状会改变吗？为什么？用四根细木棒钉成的四边形框架呢？

答案： 三角形框架的形状不会改变,根据“SSS”三角形的三个边确定,则它的形状和大小都确定.用四根细木棒钉成的四边形框架形状会改变.

练习 三角形的稳定性广泛应用于生产生活中,但有一些物品不能利用三角形稳定性,以下物品不具备三角形稳定性的是 (D)
A.自行车的三角形车架
B.三角形房架
C.照相机的三脚架
D.学校的栅栏门

答案： D

反思
用SSS证明三角形全等通常给定两边对应相等,再找第三边,怎么找呢？

答案： 1. 利用线段的和差关系：
例如：已知$AB = DE$，$AC = DF$，若$BC=BE + EC$，$EF = EC+CF$，且$BE = CF$，那么$BC = EF$。
2. 利用公共边：
如图，在$\triangle ABC$和$\triangle ADC$中，若$AB = AD$，$BC = DC$，$AC$是公共边，即$AC = AC$，则可利用$SSS$（$AB = AD$，$BC = DC$，$AC = AC$）证明$\triangle ABC\cong\triangle ADC$。
3. 利用中点或中线：
若$D$是$BC$中点，则$BD = DC$。如在$\triangle ABD$和$\triangle ACD$中，若$AB = AC$，$AD = AD$（公共边），$BD = DC$（因为$D$是$BC$中点），则可利用$SSS$证明$\triangle ABD\cong\triangle ACD$。
4. 利用等量代换：
已知$a = b$，$c = d$，且$b + e=c + e$，那么$a + e=d + e$。例如在两个三角形中，若有两组边分别相等，第三边可通过这种等量代换的关系得到相等。