《2025年全品学练考八年级数学上册苏科版江苏专版》

问题情境
根据“弦图”的思路,用4张如图3-1-8所示的直角三角形纸片拼成一个边长为c的大正方形(图3-1-9).你能用这个图形证明勾股定理吗?
如图3-1-9,大正方形的边长为c,则$S_{正方形ABCD}=$$c^{2}$.
因为大正方形是由4个直角三角形和1个边长为$b - a$的小正方形组成的,所以,大正方形的面积是4个直角三角形面积与小正方形面积的和.
即$S_{正方形ABCD}= 4×\frac {1}{2}ab+(b-a)^{2}= 2ab+b^{2}-2ab+a^{2}= a^{2}+b^{2}$.
所以$a^{2}+b^{2}= c^{2}$.

答案： $c^{2}$ $b - a$

1. 用4张如图3-1-8所示的直角三角形纸片拼成如图3-1-10所示的大正方形,你能用这个图形证明勾股定理吗?

答案： 1. 解:能.证明:图中大正方形的边长为$a + b$,则面积$=(a + b)^{2}=a^{2}+2ab + b^{2}$,
4个直角三角形的面积和$=4×\frac{1}{2}ab = 2ab$,
∴中间小正方形的面积$=a^{2}+2ab + b^{2}-2ab = a^{2}+b^{2}$.
∵中间小正方形的边长为$c$,
∴其面积为$c^{2},\therefore a^{2}+b^{2}=c^{2}$.

2. 连接图3-1-10中小正方形的对角线,可以得到图3-1-11.试利用图3-1-11中的面积关系证明勾股定理.

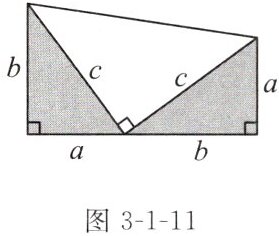
答案： 2. 证明:如图.$S_{梯形ACFD}=$
$\frac{1}{2}(AC + DF)\cdot CF=$
$\frac{1}{2}(a + b)^{2}=\frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2},$
$S_{梯形ACFD}=S_{\triangle ACB}+S_{\triangle ABD}+S_{\triangle BFD}$
$=\frac{1}{2}AC\cdot CB+\frac{1}{2}AB\cdot BD+\frac{1}{2}BF\cdot DF$
$=ab+\frac{1}{2}c^{2}.$
$\therefore \frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2}=ab+\frac{1}{2}c^{2}.$
$\therefore a^{2}+b^{2}=c^{2}.$