《2025年全品学练考八年级数学上册苏科版江苏专版》

例(教材典题)如图1-2-8,已知△ABC≌△EFD。求证：AB//EF。

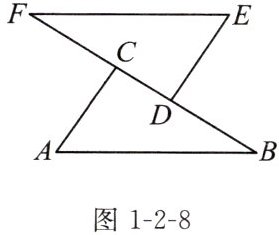
讨论 在图1-2-8中,当△DEF沿BC所在直线平移时,AB与EF仍然平行吗？为什么？

答案： 证明:
∵△ABC≌△EFD,
∴∠B=∠F(全等三角形的对应角相等).
∴AB//EF(内错角相等,两直线平行). 解:不一定,存在 AB//EF 和 AB,EF 共线两种情况.理由如下:△DEF 沿 BC 所在直线平移时,仍有△ABC≌△EFD,
∴∠ABC=∠EFD.当点 F 与点 B 不重合时,AB//EF.当点 F 与点 B 重合时,AB 与 EF 共线.

变式 如图1-2-9,已知点B,E,C,F在同一直线上,△ABC≌△DEF,AC交DE于点H,∠A = 85°,∠B = 60°,AB = 8,EH = 2。求∠F的度数与DH的长。

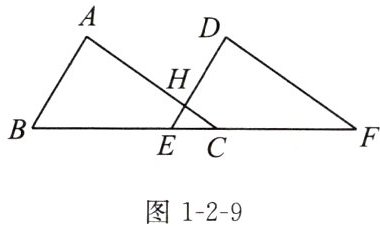
答案： ∠F=35° DH=6

反思
平移、轴对称、旋转得到直观的三角形全等模型,除此以外,还有别的全等模型吗？

答案： 有