《2025年全品学练考八年级数学上册苏科版江苏专版》

练习 下列各题要用“斜边、直角边(HL)”直接证明两个直角三角形全等.
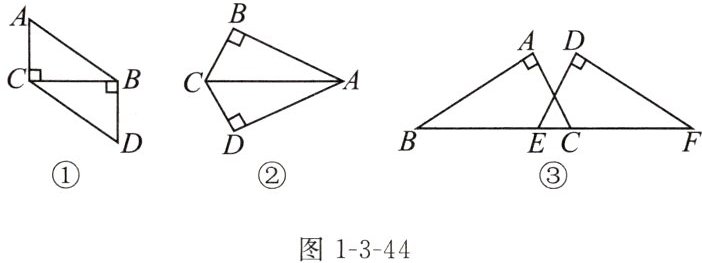
(1)如图1-3-44①,已知:$∠ACB= ∠CBD= 90^{\circ }$,则还需补充的条件是AB=CD;
(2)如图②,已知:$∠B= ∠D= 90^{\circ }$,则还需补充的条件是BC=DC（或AB=AD）;
(3)如图③,已知:点B,E,C,F在同一直线上,$∠A= ∠D= 90^{\circ },AC= DE$,则还需补充的条件是BC=FE（或BE=FC）.

答案： （1）AB=CD （2）BC=DC（或AB=AD）（3）BC=FE（或BE=FC）

例 (教材典题)如图1-3-45,AD,BC相交于点O,$AD= BC,∠C= ∠D= 90^{\circ }$.
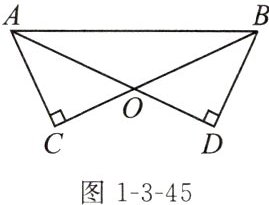
求证:$AO= BO,CO= DO$.

答案： 证明：在Rt△ACB和Rt△BDA中，
∵∠C=∠D=90°，
AB=BA（公共边），
AD=BC（已知），
∴Rt△ACB≌Rt△BDA（HL），
∴AC=BD。
在△ACO和△BDO中，
∵∠AOC=∠BOD（对顶角相等），
∠C=∠D（已知），
AC=BD（已证），
∴△ACO≌△BDO（AAS），
∴AO=BO，CO=DO。

练习1 如图1-3-46,$Rt\triangle ABE与Rt\triangle CDF$中,$∠B,∠D$是直角,边BE,DF在一条直线上,且$BF= DE,CF= AE$.求证:$CF// AE$.

答案： 证明：
∵BF=DE，
∴BF+EF=DE+EF，即DF=BE.在Rt△ABE和Rt△CDF中，{BE=DF，AE=CF，
∴Rt△ABE≌Rt△CDF（HL），
∴∠CFD=∠AEB，
∴CF//AE.