第161页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
模块1 平方根与立方根的概念与性质
(1)平方根的概念:
(2)算术平方根的概念:
(3)立方根的概念:
(4)平方根的性质:
(5)立方根的性质:
(1)平方根的概念:
如果$x^{2}=a(a\geqslant0)$,那么x叫作a的平方根
;(2)算术平方根的概念:
如果一个正数x的平方等于a,即$x^{2}=a$,那么这个正数x叫作a的算术平方根
;(3)立方根的概念:
如果$x^{3}=a$,那么x叫作a的立方根
;(4)平方根的性质:
一个正数有两个平方根,这两个平方根互为相反数;0的平方根是0;负数没有平方根
;(5)立方根的性质:
正数的立方根是正数;0的立方根是0;负数的立方根是负数
.
答案:
(1)如果$x^{2}=a(a\geqslant0)$,那么x叫作a的平方根;
(2)如果一个正数x的平方等于a,即$x^{2}=a$,那么这个正数x叫作a的算术平方根;
(3)如果$x^{3}=a$,那么x叫作a的立方根;
(4)一个正数有两个平方根,这两个平方根互为相反数;0的平方根是0;负数没有平方根;
(5)正数的立方根是正数;0的立方根是0;负数的立方根是负数
(1)如果$x^{2}=a(a\geqslant0)$,那么x叫作a的平方根;
(2)如果一个正数x的平方等于a,即$x^{2}=a$,那么这个正数x叫作a的算术平方根;
(3)如果$x^{3}=a$,那么x叫作a的立方根;
(4)一个正数有两个平方根,这两个平方根互为相反数;0的平方根是0;负数没有平方根;
(5)正数的立方根是正数;0的立方根是0;负数的立方根是负数
例1 下列说法不正确的是 (
A.4的平方根是$\pm 2$
B.正数、0和负数都有立方根
C.只有非负数才有平方根
D.-27的立方根是$-\sqrt [3]{3}$
D
)A.4的平方根是$\pm 2$
B.正数、0和负数都有立方根
C.只有非负数才有平方根
D.-27的立方根是$-\sqrt [3]{3}$
答案:
D
模块2 实数的相关概念
(1)无理数的概念:
(2)实数的概念:
(3)实数与数轴上点的关系:
(1)无理数的概念:
无限不循环小数叫作无理数
;(2)实数的概念:
有理数和无理数统称为实数
;(3)实数与数轴上点的关系:
一一对应
.
答案:
(1)无限不循环小数叫作无理数;
(2)有理数和无理数统称为实数;
(3)一一对应
(1)无限不循环小数叫作无理数;
(2)有理数和无理数统称为实数;
(3)一一对应
例2 下列说法中错误的是 (
A.$\sqrt [3]{-27}$是整数
B.$-\frac {17}{13}$是有理数
C.$\frac {\sqrt {3}}{3}$是分数
D.$\sqrt {9}$的立方根是无理数
C
)A.$\sqrt [3]{-27}$是整数
B.$-\frac {17}{13}$是有理数
C.$\frac {\sqrt {3}}{3}$是分数
D.$\sqrt {9}$的立方根是无理数
答案:
C
例3 $\sqrt {3}-\sqrt {5}$的相反数为
$\sqrt{5}-\sqrt{3}$
,$|1-\sqrt {2}|= $$\sqrt{2}-1$
,绝对值为$\sqrt [3]{27}$的数为$\pm3$
.
答案:
$\sqrt{5}-\sqrt{3}$,$\sqrt{2}-1$,$\pm3$
例4 从下列各数中,选择合适的数填空.
$-4.1,\sqrt [3]{0.008},0,|-\sqrt {6}|,π,\sqrt [3]{6},\frac {1}{7},-\sqrt {81}.$
(1)无理数为
(2)如图2-T-1,被阴影覆盖的数为
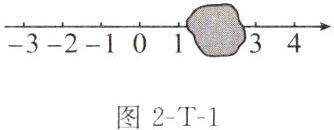
(3)平方根等于本身的数为
(4)将一个长、宽、高分别为3米、2米、2米的长方体铁块熔化,制成两个完全相同的正方体铁块,则该正方体铁块的棱长为
$-4.1,\sqrt [3]{0.008},0,|-\sqrt {6}|,π,\sqrt [3]{6},\frac {1}{7},-\sqrt {81}.$
(1)无理数为
$|-\sqrt{6}|$,$\pi$,$\sqrt[3]{6}$
;(2)如图2-T-1,被阴影覆盖的数为
$|-\sqrt{6}|$,$\sqrt[3]{6}$
;
(3)平方根等于本身的数为
0
;(4)将一个长、宽、高分别为3米、2米、2米的长方体铁块熔化,制成两个完全相同的正方体铁块,则该正方体铁块的棱长为
$\sqrt[3]{6}$
米.
答案:
(1)$|-\sqrt{6}|$,$\pi$,$\sqrt[3]{6}$;
(2)$|-\sqrt{6}|$,$\sqrt[3]{6}$;
(3)0;
(4)$\sqrt[3]{6}$
(1)$|-\sqrt{6}|$,$\pi$,$\sqrt[3]{6}$;
(2)$|-\sqrt{6}|$,$\sqrt[3]{6}$;
(3)0;
(4)$\sqrt[3]{6}$
例5 已知a的算术平方根为3,ab的立方根为-3,b和c互为相反数.
(1)求a,b,c的值;
(2)求$a+2b+c$的平方根.
(1)求a,b,c的值;
(2)求$a+2b+c$的平方根.
答案:
(1)$a=9$ $b=-3$ $c=3$;
(2)$\pm\sqrt{6}$
(1)$a=9$ $b=-3$ $c=3$;
(2)$\pm\sqrt{6}$
查看更多完整答案,请扫码查看


