《2025年全品学练考八年级数学上册苏科版江苏专版》

找出下列各数中的无理数,并把它们填入图2-3-2的方框中.
$\sqrt {\frac {9}{16}},-\frac {24}{7},\sqrt {3},\sqrt [3]{8},-\sqrt {2},π+3.$

答案： 解：无理数为$\sqrt{3},-\sqrt{2},\pi+3$．$\sqrt{3}$和$\pi+3$都是正数．由$1＜\sqrt{3}＜\sqrt{4}$，知$1＜\sqrt{3}＜2$；$\pi+3＞6$．所以方框中从左到右依次填$-\sqrt{2},\sqrt{3},\pi+3$．

例2(教材典题)找一个有理数a,使$\sqrt {2}＜a＜\sqrt {3}$.
探究 你能找到一个无理数a,使$\sqrt {2}＜a＜\sqrt {3}$吗?

答案： 解：符合条件的有理数有无穷多个．$\because 2＜1.5^{2}＜3$，$\therefore \sqrt{2}＜1.5＜\sqrt{3}$．$\therefore$取$a=1.5$．
探究 解：符合条件的无理数有无穷多个．$\because 2＜\frac{5}{2}＜3$，$\therefore \sqrt{2}＜\sqrt{\frac{5}{2}}＜\sqrt{3}$．$\therefore$取$a=\sqrt{\frac{5}{2}}$．

课堂总结与反思

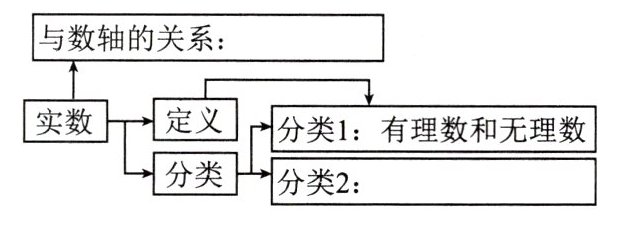
答案：

与数轴的关系：每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都表示一个实数，即实数和数轴上的点一一对应。

分类2：正实数、零、负实数。

反思
如何看待实数与数轴上点的一一对应的关系?

答案： 实数与数轴上的点一一对应，即每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都表示一个实数。
这种一一对应关系具有重要意义：
- 从几何角度看，它将抽象的实数概念直观地用数轴上的点来体现，使实数有了直观的几何形象。
- 从代数角度看，通过数轴可以更方便地研究实数的性质，如大小比较（数轴上右边的点表示的数总比左边的点表示的数大）、运算等。
- 它是数学中数形结合思想的重要体现，为解决数学问题提供了有力的工具和方法。例如，在求解不等式、方程等问题时，可以借助数轴来直观地分析和理解。
总之，实数与数轴上点的一一对应关系是数学中非常基础且关键的内容，对数学的学习和研究有着深远的影响。