《2025年全品学练考八年级数学上册苏科版江苏专版》

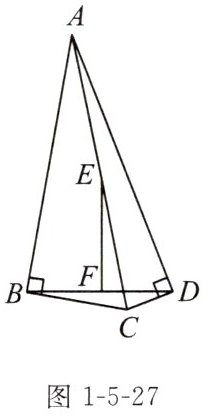
拓展 已知：如图1-5-27,∠ABC= ∠ADC= 90°,E,F分别是AC,BD的中点.
(1)求证：EF⊥BD；
(2)若∠BAD= 30°,AC= 8,求BD的长.

答案：
(1)略
(2)4

反思
直角三角形的性质定理是运用等边三角形的性质推导出来的吗？

答案： 【解析】：
本题主要考查直角三角形的性质定理及其运用。直角三角形的性质定理并不是通过等边三角形的性质推导出来的，而是基于直角三角形的特性和几何关系进行推导。在直角三角形中，最重要的性质定理是勾股定理，它表明直角三角形的两条直角边的平方和等于斜边的平方。此外，直角三角形还具有一些其他的性质，如直角边上的中线等于该边的一半，30°-60°-90°直角三角形的边长比例关系等。
对于题目中的“反思”部分，需要明确的是，直角三角形的性质定理并不是由等边三角形的性质推导出来的。两者虽然都是三角形，但它们的性质和定理是基于各自的特性和几何关系进行推导的，因此，直角三角形的性质定理的运用并不依赖于等边三角形的性质。
【答案】：
直角三角形的性质定理不是运用等边三角形的性质推导出来的。

1. 若$\triangle ABC三边长为a,b,c$,则有$|b - c| ＜ a ＜$b + c,$|a - c| ＜ b ＜$a + c,|a - b|$＜ c ＜ a + b$。

答案： b + c，a + c，|a - b|

2. 在$\triangle ABC$中,若$AB ＞ AC$,则$\angle B$＜$\angle C$。

答案： ＜

例1 长度为$2cm$,$3cm$,$4cm$,$5cm$的4条线段,若以其中的3条线段为边构成三角形,可以构成不同的三角形共有(C)
A.1个
B.2个
C.3个
D.4个

答案： C