《2025年全品学练考八年级数学上册苏科版江苏专版》

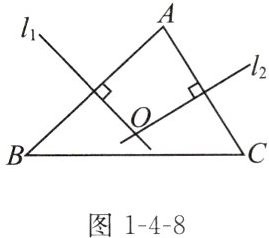
例(教材典题)如图1-4-8,在△ABC中,AB,AC的垂直平分线$l_1,l_2$相交于点O。求证：点O在BC的垂直平分线上。

答案：
证明:如图,连接OA,OB,OC.
∵点O在AB的垂直平分线
l₁上,

∴OA=OB(线段垂直平分线的性质定理).
同理,OA=OC.
∴OB=OC.
∴点O在BC的垂直平分线上(线段垂直平分线性质定理的逆定理).

反思
线段垂直平分线性质定理在解作图问题中有哪些应用？

答案： 求作最短路径,解台球碰撞问题等.

问题探究
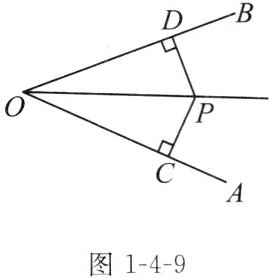
如图1-4-9,在∠AOB的平分线上任意取一点P,分别画点P到OA和OB的垂线段PC和PD,垂足分别为C,D.PC与PD一定相等吗？如何证明？
证明：在△DOP和△COP中,由∠PDO= ∠PCO= 90°,∠DOP= ∠COP,OP= OP,通过“AAS”,可以证明△DOP≌△COP,所以PC与PD相等.

答案： PCO 90 COP AAS

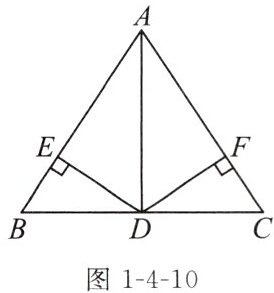
例1 如图1-4-10,在△ABC中,AD平分∠BAC,交边BC于点D,D为BC中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,若BE= 2,求CF的长.

答案： 2