《2025年全品学练考八年级数学上册苏科版江苏专版》

拓展 已知一个正数的两个平方根分别为$2m-3$,$6+m$,求这个正数.

答案： 25

例2 求下列各式中的x：
(1)$2x^{2}= 32$； (2)$\frac {1}{2}(x+2)^{2}= 7$.

答案：
(1)±4
(2)-2+√14或-2-√14

讨论 (1)如图2-1-2①,将面积为2的正方形纸片放置在面积为3的正方形纸片上,据图比较$\sqrt {2}与\sqrt {3}$的大小；
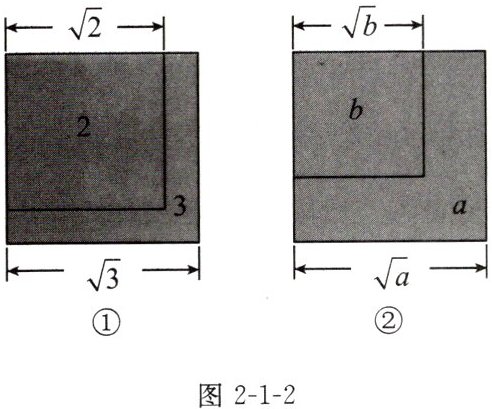
(2)已知$a＞b＞0$,类似地,根据图②比较$\sqrt {a}与\sqrt {b}$的大小.

答案： 解:
(1)√2＜√3.
(2)√a＞√b.

练习 比较下列各组数的大小：
(1)$\sqrt {5}$＞$\sqrt {2}$；(2)$\sqrt {7}$＜$\sqrt {11}$；(3)$\sqrt {12.3}$＞$\sqrt {10.3}$；
(4)$\sqrt {3}$＞$\sqrt {\frac {3}{2}}$；(5)$\sqrt {2\frac {1}{2}}$＜$\sqrt {3\frac {1}{3}}$；(6)$\sqrt {0.5}$＞$\sqrt {0.07}$.

答案：
(1)＞
(2)＜
(3)＞
(4)＞
(5)＜
(6)＞

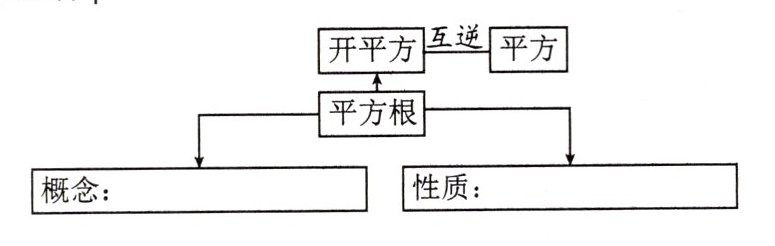
课堂总结与反思

答案： 1. **概念**：
如果$x^{2}=a(a\geq0)$，那么$x$叫做$a$的平方根，记作$x = \pm\sqrt{a}$。
2. **性质**：
正数有两个平方根，它们互为相反数；$0$的平方根是$0$；负数没有平方根。
即概念：若$x^{2}=a(a\geq0)$，则$x$叫$a$的平方根（$x = \pm\sqrt{a}$）；性质：正数有两个互为相反数的平方根，$0$的平方根是$0$，负数无平方根。

反思
如何求一个数的平方根？

答案： 解:求一个数的平方根,通常借助平方运算,逆向得出.