第133页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
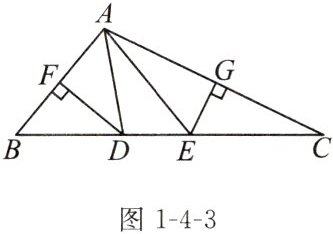
练习 如图1-4-3,△ABC中,AB,AC边的垂直平分线分别交BC于点D,E,垂足分别为F,G,△ADE的周长为5,求BC的长。

答案:
5
问题探究
如果一个点到一条线段两端的距离相等,那么这个点一定在这条线段的垂直平分线上吗?如何证明?
证明:如图1-4-5,当点Q在线段AB上时,如果QA=QB,那么Q是线段AB的
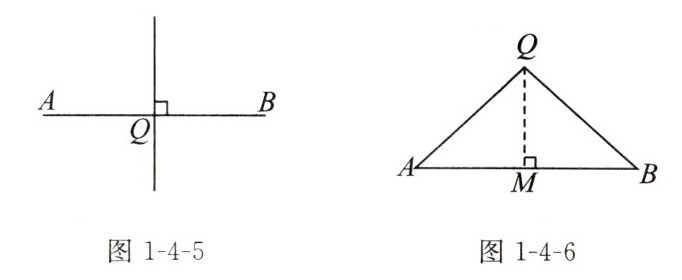
如图1-4-6,当点Q在线段AB外时,作QM⊥AB,垂足为M,∠QMA=∠
如果一个点到一条线段两端的距离相等,那么这个点一定在这条线段的垂直平分线上吗?如何证明?
证明:如图1-4-5,当点Q在线段AB上时,如果QA=QB,那么Q是线段AB的
中
点,所以线段AB的垂直平分线一定经过点Q。
如图1-4-6,当点Q在线段AB外时,作QM⊥AB,垂足为M,∠QMA=∠
QMB
=90°。如果QA=QB,那么通过“______HL
”,可以证明Rt△QAM≌Rt△QBM,所以AM=______BM
,即M是线段AB的______中
点,所以QM是线段AB的垂直平分线,即点Q一定在线段AB的垂直平分线上。
答案:
中 QMB HL BM 中
讨论探究
如图1-4-7,AB= AD,CB= CD,AC,BD相交于点E。你能在图中找到哪些相等的角?如何证明?
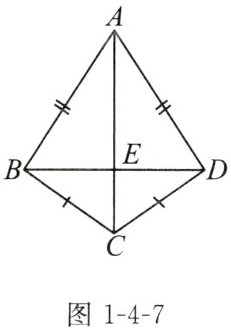
如图1-4-7,AB= AD,CB= CD,AC,BD相交于点E。你能在图中找到哪些相等的角?如何证明?

答案:
解:相等的角:∠AED=∠AEB=∠CED=∠CEB,∠DAC=∠BAC,∠ACD=∠ACB,∠ADC=∠ABC,∠ADE=∠ABE,∠CDE=∠CBE.
证明如下:
∵AB=AD,CB=CD,
∴AC 垂直平分线段 BD.
∴∠AEB=∠AED=∠BEC=∠DEC=90°.
在△ADC和△ABC中,AD=AB,
CD=CB,
AC=AC,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,∠ACD=∠ACB,∠ADC=∠ABC.
在△ADE和△ABE中,AD=AB,
∠DAE=∠BAE,
AE=AE,
∴△ADE≌△ABE(SAS).
∴∠ADE=∠ABE.
∴∠CDE=∠CBE.
证明如下:
∵AB=AD,CB=CD,
∴AC 垂直平分线段 BD.
∴∠AEB=∠AED=∠BEC=∠DEC=90°.
在△ADC和△ABC中,AD=AB,
CD=CB,
AC=AC,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,∠ACD=∠ACB,∠ADC=∠ABC.
在△ADE和△ABE中,AD=AB,
∠DAE=∠BAE,
AE=AE,
∴△ADE≌△ABE(SAS).
∴∠ADE=∠ABE.
∴∠CDE=∠CBE.
查看更多完整答案,请扫码查看


