第148页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质,还具有性质定理:
等边三角形的判定定理:1.
等边三角形的各角都等于60°
。等边三角形的判定定理:1.
三个角都相等的三角形是等边三角形
。2. 有一个角是60°的等腰三角形是等边三角形
。
答案:
等边三角形的各角都等于60°;1. 三个角都相等的三角形是等边三角形;2. 有一个角是60°的等腰三角形是等边三角形
例9 如图1-T-7,$\triangle ABC$是等边三角形,$BD \perp AC$,$AE \perp BC$,垂足分别为$D,E$,$AE与BD相交于点O$,连接$DE$。
(1)判断$\triangle CDE$的形状,并说明理由;
(2)若$AO = 12$,求$OE$的长。
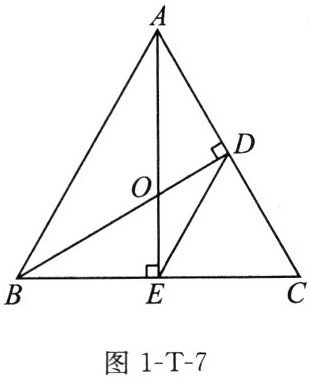
(1)判断$\triangle CDE$的形状,并说明理由;
(2)若$AO = 12$,求$OE$的长。

答案:
(1)△ADE是等边三角形 理由略;
(2)6
(1)△ADE是等边三角形 理由略;
(2)6
含$30^{\circ}$角的直角三角形的性质:
直角三角形的性质定理:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边是斜边的一半
。直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半
。
答案:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边是斜边的一半;直角三角形斜边上的中线等于斜边的一半
例10 如图1-T-8,在$Rt \triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle B = 30^{\circ}$,$AC = 2$,$CD$是斜边上的中线,$CE$是高,$F是CD$的中点,连接$EF$。
(1)求线段$CD$的长;
(2)求证:$\triangle EDF$是等边三角形。
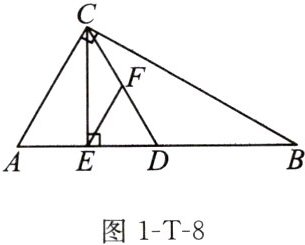
(1)求线段$CD$的长;
(2)求证:$\triangle EDF$是等边三角形。

答案:
(1)2;
(2)略
(1)2;
(2)略
例11 在$Rt \triangle ABC$中,$AC = BC$,$\angle ACB = 90^{\circ}$,$O为AB$的中点。
(1)若$\angle EOF = 90^{\circ}$,两边分别交直线$AC$,$BC于点E,F$。
①如图1-T-9①,当点$E,F分别在边AC和BC$上时,求证:$OE = OF$;
②如图②,当点$E,F分别在AC和CB$的延长线上时,连接$EF$,若$OE = 6$,求$S_{\triangle EOF}$。
(2)如图③,若$\angle EOF = 45^{\circ}$,两边分别交边$AC于点E$,交$BC的延长线于点F$,连接$EF$,若$CF = 3$,$EF = 5$,试求$AE$的长。
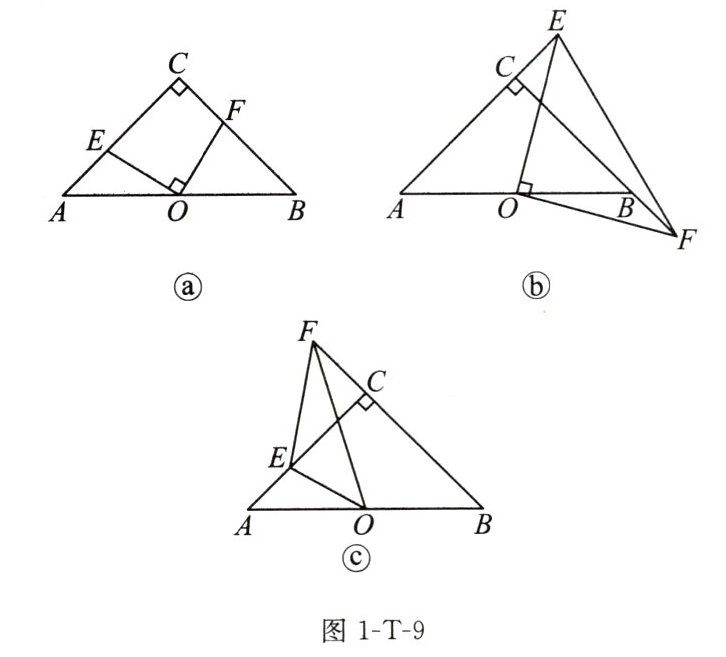
(1)若$\angle EOF = 90^{\circ}$,两边分别交直线$AC$,$BC于点E,F$。
①如图1-T-9①,当点$E,F分别在边AC和BC$上时,求证:$OE = OF$;
②如图②,当点$E,F分别在AC和CB$的延长线上时,连接$EF$,若$OE = 6$,求$S_{\triangle EOF}$。
(2)如图③,若$\angle EOF = 45^{\circ}$,两边分别交边$AC于点E$,交$BC的延长线于点F$,连接$EF$,若$CF = 3$,$EF = 5$,试求$AE$的长。

答案:
解:
(1)①证明:如图a,连接OC.
∵AC = BC,∠ACB = 90°,O为AB的中点,
∴AO = CO = BO,∠AOC = 90°,∠A = ∠BCO = 45°.
∵∠EOF = 90°,
∴∠AOE = ∠COF,
∴△AOE ≌ △COF(ASA),
∴OE = OF. ②如图b,连接OC.
∵AC = BC,∠ACB = 90°,O为AB的中点,
∴AO = CO = BO,∠BOC = 90°,∠ABC = ∠ACO = 45°,
∴∠OCE = ∠OBF = 135°.
∵∠COB = ∠EOF = 90°,
∴∠COE = ∠BOF,
∴△COE ≌ △BOF(ASA),
∴OF = OE = 6,
∴S△EOF = 1/2OE·OF = 18.
(2)如图c,连接CO,过点O作HO⊥FO,交CA的延长线于点H.
∵AC = BC,∠ACB = 90°,O为AB的中点,
∴AO = CO = BO,∠AOC = 90°,∠BAC = ∠BCO = 45°,
∴∠OCF = ∠OAH = 135°.
∵HO⊥FO,
∴∠FOH = 90°,
∴∠FOH = ∠AOC,
∴∠COF = ∠AOH,
∴△COF ≌ △AOH(ASA),
∴AH = CF = 3,OF = OH.
∵∠EOF = 45°,∠FOH = 90°,
∴∠EOF = ∠EOH = 45°. 又
∵OF = OH,EO = EO,
∴△EOF ≌ △EOH(SAS),
∴EH = EF = 5,
∴AE = EH - AH = 2.
(1)①证明:如图a,连接OC.
∵AC = BC,∠ACB = 90°,O为AB的中点,
∴AO = CO = BO,∠AOC = 90°,∠A = ∠BCO = 45°.
∵∠EOF = 90°,
∴∠AOE = ∠COF,
∴△AOE ≌ △COF(ASA),
∴OE = OF. ②如图b,连接OC.
∵AC = BC,∠ACB = 90°,O为AB的中点,
∴AO = CO = BO,∠BOC = 90°,∠ABC = ∠ACO = 45°,
∴∠OCE = ∠OBF = 135°.
∵∠COB = ∠EOF = 90°,
∴∠COE = ∠BOF,
∴△COE ≌ △BOF(ASA),
∴OF = OE = 6,
∴S△EOF = 1/2OE·OF = 18.
(2)如图c,连接CO,过点O作HO⊥FO,交CA的延长线于点H.
∵AC = BC,∠ACB = 90°,O为AB的中点,
∴AO = CO = BO,∠AOC = 90°,∠BAC = ∠BCO = 45°,
∴∠OCF = ∠OAH = 135°.
∵HO⊥FO,
∴∠FOH = 90°,
∴∠FOH = ∠AOC,
∴∠COF = ∠AOH,
∴△COF ≌ △AOH(ASA),
∴AH = CF = 3,OF = OH.
∵∠EOF = 45°,∠FOH = 90°,
∴∠EOF = ∠EOH = 45°. 又
∵OF = OH,EO = EO,
∴△EOF ≌ △EOH(SAS),
∴EH = EF = 5,
∴AE = EH - AH = 2.
查看更多完整答案,请扫码查看


