第164页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
问题探究
如图3-1-1,以Rt△ABC的三边为边分别向外画一个正方形,所画的三个正方形面积之间有怎样的数量关系?
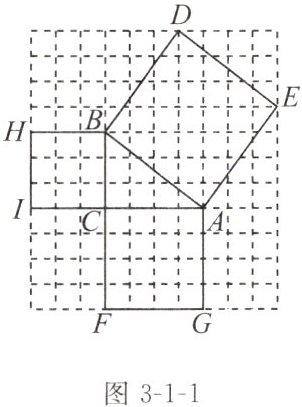
设小正方形的边长均为1,正方形BHIC、正方形ACFG的面积分别为
因为$S_{正方形AEDB}= AB^{2},S_{正方形BHIC}=$
所以$AB^{2}=$
即Rt△ABC
如图3-1-1,以Rt△ABC的三边为边分别向外画一个正方形,所画的三个正方形面积之间有怎样的数量关系?

设小正方形的边长均为1,正方形BHIC、正方形ACFG的面积分别为
9
和16
,正方形AEDB的面积为25
,三个正方形面积之间的关系为$S_{正方形AEDB}= S_{正方形BHIC}+$$ S_{正方形ACFG} $
.因为$S_{正方形AEDB}= AB^{2},S_{正方形BHIC}=$
$ BC^2 $
,$S_{正方形ACFG}= AC^{2},$所以$AB^{2}=$
$ BC^2 $
+$ AC^2 $
.即Rt△ABC
两条直角边的平方和
等于斜边的平方.
答案:
9 16 25 $ S_{正方形ACFG} $ $ BC^2 $ $ BC^2 $ $ AC^2 $ 两条直角边的平方和
在下面的方格纸上,任意画一个顶点都在格点上的直角三角形,并分别以这个直角三角形的各边为一边向三角形外部作正方形,仿照上面的方法找出三个正方形面积之间的关系,并与同学交流.

答案:
解:画图略.两个较小的正方形的面积和等于较大正方形的面积.
查看更多完整答案,请扫码查看


