第128页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
问题情境
如图1-3-32,要使△ABD≌△ACD,
(1)根据“SAS”需添加的两个条件是
(2)根据“ASA”需添加的两个条件是
(3)根据“AAS”需添加的两个条件是
(4)根据“SSS”需添加的两个条件是
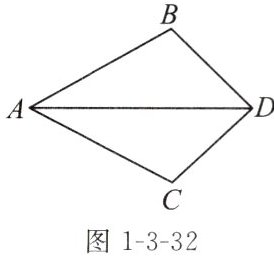
如图1-3-32,要使△ABD≌△ACD,
(1)根据“SAS”需添加的两个条件是
AB=AC,∠BAD=∠CAD(也可以是BD=CD,∠BDA=∠CDA)
;(2)根据“ASA”需添加的两个条件是
∠BAD=∠CAD,∠BDA=∠CDA
;(3)根据“AAS”需添加的两个条件是
∠BAD=∠CAD,∠B=∠C(也可以是∠BDA=∠CDA,∠B=∠C)
;(4)根据“SSS”需添加的两个条件是
AB=AC,BD=CD
.
答案:
(1)AB=AC,∠BAD=∠CAD(也可以是BD=CD,∠BDA=∠CDA)
(2)∠BAD=∠CAD,∠BDA=∠CDA
(3)∠BAD=∠CAD,∠B=∠C(也可以是∠BDA=∠CDA,∠B=∠C)
(4)AB=AC,BD=CD
(1)AB=AC,∠BAD=∠CAD(也可以是BD=CD,∠BDA=∠CDA)
(2)∠BAD=∠CAD,∠BDA=∠CDA
(3)∠BAD=∠CAD,∠B=∠C(也可以是∠BDA=∠CDA,∠B=∠C)
(4)AB=AC,BD=CD
例1(教材典题)如图1-3-33,点E在BD上,AB= BC,AE= CE.
求证:AD= CD.
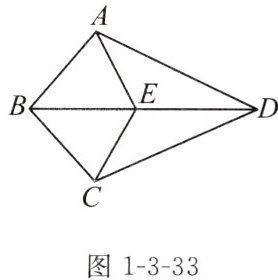
求证:AD= CD.

答案:
证明:在△ABE和△CBE中,AB=CB,BE=BE,AE=CE,
∴△ABE≌△CBE(SSS).
∴∠ABE=∠CBE.
在△ABD和△CBD中,AB=CB,∠ABD=∠CBD,BD=BD,
∴△ABD≌△CBD(SAS).
∴AD=CD.
∴△ABE≌△CBE(SSS).
∴∠ABE=∠CBE.
在△ABD和△CBD中,AB=CB,∠ABD=∠CBD,BD=BD,
∴△ABD≌△CBD(SAS).
∴AD=CD.
练习1 如图1-3-34,AB,CD相交于点O,AD= CB,AB= CD,连接DB.
求证:OD= OB.
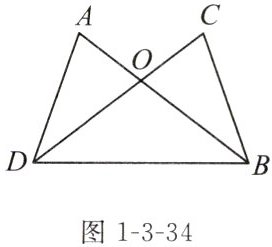
求证:OD= OB.

答案:
证明:在△ABD与△CDB中,AB=CD,BD=DB,AD=CB,
∴△ABD≌△CDB(SSS),
∴∠A=∠C.
在△AOD与△COB中,∠A=∠C,∠AOD=∠COB,AD=CB,
∴△AOD≌△COB(AAS).
∴OD=OB.
∴△ABD≌△CDB(SSS),
∴∠A=∠C.
在△AOD与△COB中,∠A=∠C,∠AOD=∠COB,AD=CB,
∴△AOD≌△COB(AAS).
∴OD=OB.
练习2 如图1-3-35,AD,BF相交于点O,点E,C在BF上,BE= FC,AB//DF,AC//DE.求证:AO= DO,CO= EO.
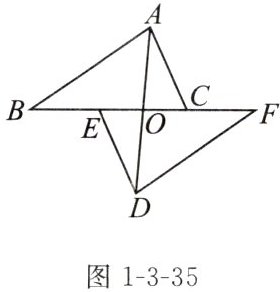

答案:
证明:
∵AB//DF,
∴∠B=∠F(两直线平行,内错角相等).
∵AC//DE,
∴∠ACB=∠DEF(两直线平行,内错角相等).
∵BE=FC,
∴BE+EC=FC+EC,即BC=FE.
在△ABC和△DFE中,
$\begin{cases} ∠B=∠F \\ BC=FE \\ ∠ACB=∠DEF \end{cases}$
∴△ABC≌△DFE(ASA).
∴AC=DE(全等三角形对应边相等).
在△AOC和△DOE中,
$\begin{cases} ∠ACO=∠DEO(对顶角相等) \\ AC=DE \\ ∠AOC=∠DOE(对顶角相等) \end{cases}$
∴△AOC≌△DOE(ASA).
∴AO=DO,CO=EO(全等三角形对应边相等).
∵AB//DF,
∴∠B=∠F(两直线平行,内错角相等).
∵AC//DE,
∴∠ACB=∠DEF(两直线平行,内错角相等).
∵BE=FC,
∴BE+EC=FC+EC,即BC=FE.
在△ABC和△DFE中,
$\begin{cases} ∠B=∠F \\ BC=FE \\ ∠ACB=∠DEF \end{cases}$
∴△ABC≌△DFE(ASA).
∴AC=DE(全等三角形对应边相等).
在△AOC和△DOE中,
$\begin{cases} ∠ACO=∠DEO(对顶角相等) \\ AC=DE \\ ∠AOC=∠DOE(对顶角相等) \end{cases}$
∴△AOC≌△DOE(ASA).
∴AO=DO,CO=EO(全等三角形对应边相等).
查看更多完整答案,请扫码查看


