《2025年全品学练考八年级数学上册苏科版江苏专版》

例2(教材补充例题)求下列各式中的x：
(1)$x^{3}= -0.125$； (2)$8x^{3}= 27$； (3)$x^{3}+3= 2$； (4)$(x-1)^{3}= 8$.

答案：
(1)-0.5
(2)$\frac{3}{2}$
(3)-1
(4)3

例3(教材补充例题)把一个长12cm、宽9cm、高2cm的长方体铁坯加工成一个正方体铁锭后,表面积有什么变化？(加工过程中无损失)

答案： 减少了$84\ cm^2$

课堂总结与反思

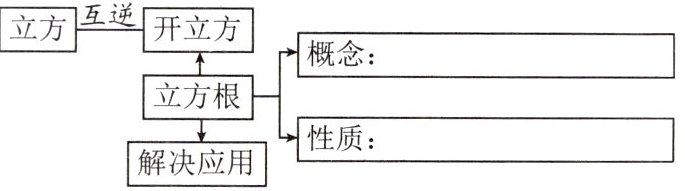
答案： 1. 首先明确立方根的概念：
一般地，如果一个数$x$的立方等于$a$，即$x^{3}=a$，那么这个数$x$就叫做$a$的立方根（也叫做三次方根），记作$\sqrt[3]{a}$，读作“三次根号$a$”，其中$a$是被开方数，$3$是根指数。
2. 然后看立方根的性质：
正数的立方根是正数，例如：因为$2^{3}=8$，所以$\sqrt[3]{8}=2$；
负数的立方根是负数，例如：因为$( - 2)^{3}=-8$，所以$\sqrt[3]{-8}=-2$；
$0$的立方根是$0$，因为$0^{3}=0$，所以$\sqrt[3]{0}=0$。
所以概念为：如果$x^{3}=a$，那么$x$叫做$a$的立方根，记作$\sqrt[3]{a}$；性质为：正数的立方根是正数，负数的立方根是负数，$0$的立方根是$0$。

反思
立方根与平方根有何异同？

答案： 立方根与平方根的异同：
相同点：
1. 都是开方运算，与乘方运算互为逆运算；
2. 0的平方根和立方根都是0。
不同点：
1. 定义不同：平方根是平方运算的逆运算，立方根是立方运算的逆运算；
2. 表示不同：平方根用$\pm\sqrt{a}(a\geq0)$表示，立方根用$\sqrt[3]{a}$表示；
3. 个数不同：正数有两个平方根（互为相反数），负数没有平方根；任何数都有且只有一个立方根；
4. 取值范围不同：平方根中被开方数$a\geq0$，立方根中被开方数$a$为任意实数。

问题情境
我们知道,所有的分数可以写成有限小数或者循环小数的形式.例如:
$\frac {5}{2}= 2.5,\frac {5}{8}= 0.625,-\frac {1}{3}= -0.\dot {3},\frac {3}{22}= 0.\dot {1}\dot {3}\dot {6},\frac {2}{7}= 0.\dot {2}8571\dot {4}.$
是不是所有的数都可以写成有限小数或者循环小数呢?
事实上,有很多的数都不能用有限小数或者循环小数的形式表示,例如圆周率π.π就是一个无限不循环小数.

答案： 不能 不循环