《2025年全品学练考八年级数学上册苏科版江苏专版》

线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端的距离相等。
线段垂直平分线性质定理的逆定理：到线段两端距离相等的点在线段的垂直平分线上。

答案： 线段垂直平分线上的点到线段两端的距离相等；到线段两端距离相等的点在线段的垂直平分线上

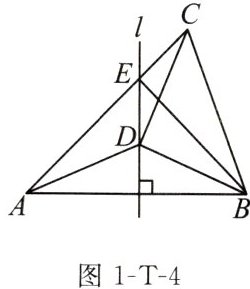
例6 如图1-T-4,在$\triangle ABC$中,$l是AB$的垂直平分线,与边$AC交于点E$,点$D在l$上,且$DB = DC$,连接$AD$。
(1)求证：$\angle CAD = \angle ACD$；
(2)连接$BE$,若$BD \perp CD$,求证：$BE \perp AC$。

答案： 证明:
(1)
∵l是AB的垂直平分线，点D在l上，
∴DA = DB.
∵DB = DC，
∴DA = DC，
∴∠CAD = ∠ACD.
(2)
∵BD⊥CD，
∴∠CDB = 90°，
∴∠BCD + ∠CBD = 90°，
∴∠CAD + ∠ACD + ∠BAD + ∠ABD = 90°.
∵DA = DB，
∴∠ABD = ∠BAD.
∵∠CAD = ∠ACD，
∴∠CAD + ∠BAD = 45°，即∠EAB = 45°.
∵l是AB的垂直平分线，
∴EA = EB，
∴∠EBA = 45°，
∴∠AEB = 90°，
∴BE⊥AC.

角平分线的性质定理：角平分线上的点到角两边的距离相等。
角平分线性质定理的逆定理：角的内部到角两边距离相等的点在角的平分线上。

答案： 角平分线上的点到角两边的距离相等；角的内部到角两边距离相等的点在角的平分线上

例7 图1-T-5①是一个平分角的仪器,其中$OD = OE$,$FD = FE$。
(1)如图②,将仪器放置在$\triangle ABC$上,使点$O与顶点A$重合,$D,E分别在边AB,AC$上,沿$AF画一条射线AP$,交$BC于点P$。$AP是\angle BAC$的平分线吗？请判断并说明理由；
(2)如图③,在(1)的条件下,过点$P作PQ \perp AB于点Q$,若$PQ = 4$,$AC = 6$,求$\triangle APC$的面积。

答案：
(1)AP是∠BAC的平分线 理由略；
(2)12

等腰三角形的性质定理：
1. 等腰三角形的两底角相等(简称“等边对等角”)。
2. 等腰三角形底边上的高线、中线及顶角平分线重合(简称“三线合一”)。
等腰三角形的判定定理：有两个角相等的三角形是等腰三角形(简称“等角对等边”)。

答案： 1. 等腰三角形的两底角相等(简称“等边对等角”)；2. 等腰三角形底边上的高线、中线及顶角平分线重合(简称“三线合一”)；有两个角相等的三角形是等腰三角形(简称“等角对等边”)

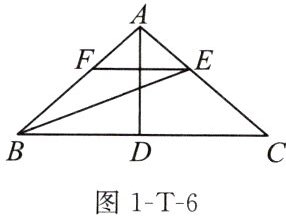
例8 如图1-T-6,在$\triangle ABC$中,$AB = AC$,$D是BC$边的中点,连接$AD$,$BE平分\angle ABC交AC于点E$。
(1)若$\angle C = 36^{\circ}$,则$\angle BAD$的度数为54°；
(2)过点$E作EF // BC交AB于点F$,求证：$FB = FE$。

答案：
(1)54°；
(2)略