《2025年全品学练考八年级数学上册苏科版江苏专版》

问题探究
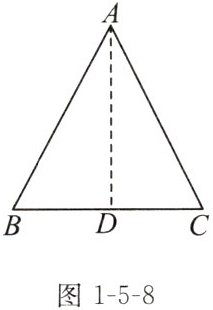
我们知道,等腰三角形的两底角相等。反过来,有两个角相等的三角形一定是等腰三角形吗？
如图1-5-8,在△ABC中,∠B= ∠C。作△ABC的角平分线AD。由∠BAD= ∠CAD,∠B= ∠C,AD= AD,可得△ABD≌△ACD。所以AB= AC。

答案： BAD B ACD

例1(教材典题)如图1-5-9,∠EAC是△ABC的外角,AD平分∠EAC,AD//BC。
求证：AB= AC。

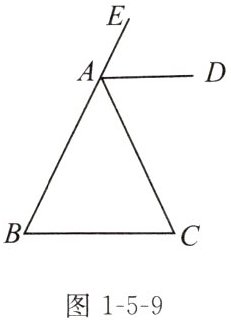
探究 在图1-5-9中,如果AB= AC,AD//BC,那么AD平分∠EAC吗？请证明你的结论。

答案： 例1 略 探究 AD 平分∠EAC 证明略

变式 如图1-5-10,在△ABC中,∠ABC,∠ACB的平分线相交于点D,过点D作EF//BC交AB于点E,交AC于点F。
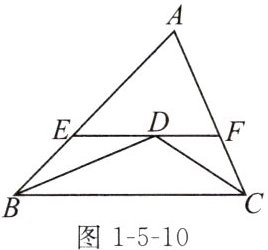
求证：BE+CF= EF。

答案： 【解析】：本题考查了等腰三角形的判定与性质，证明线段相等，通过证明角相等推出三角形为等腰三角形是常用方法之一，要熟练掌握并灵活运用。本题证明的依据是角平分线的定义，平行线的性质，以及等角对等边。
先根据角平分线的定义及平行线的性质证明$\triangle BED$和$\triangle CDF$是等腰三角形，再由等腰三角形的性质得$BE=DE$，$CF=DF$，进而可得出结论$BE+CF=EF$。
【答案】：证明：
∵$BD$平分$\angle ABC$，
∴$\angle EBD = \angle DBC$。
∵$EF// BC$，
∴$\angle EDB = \angle DBC$（两直线平行，内错角相等）。
∴$\angle EBD = \angle EDB$（等量代换）。
∴$BE = DE$（等角对等边）。
同理可得$CF = DF$。
∴$BE + CF = DE + DF = EF$。