第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
1. 如图 Z-2-1 所示,物体重为 210 N,动滑轮重为 25 N。工人用 125 N 的拉力将物体匀速提升 3 m,用了 10 s,此过程中,有用功是______J,拉力的功率是______W,滑轮的机械效率是______,克服动滑轮重所做的额外功占总功的______。




答案:
630 75 84% 10%
2. (2023 无锡滨湖区校级二模)起重机吊臂上的滑轮组如图 Z-2-2 所示。在匀速起吊重 $ 2.4 × 10^{4} $ N 的物体时,物体在 5 s 内上升了 5 m,此过程中有用功为______J,钢丝绳移动的速度为______m/s;若滑轮组的机械效率为 80%,拉力 $ F $ 大小为______N,克服绳重、摩擦所做的功为 $ 2.4 × 10^{4} $ J,则动滑轮重______N。
答案:
$1.2×10^{5}$ 3 $1×10^{4}$ 1200
3. (2024 南通)如图 Z-2-3 所示,工人用 330 N 的拉力,使用定滑轮将质量为 30 kg 的物体 6 s 内匀速吊起 3 m,g 取 10 N/kg。求:
(1)物体上升的速度。
(2)工人做功的功率。
(3)定滑轮的机械效率。(结果精确到 $ 0.1 \% $)

(1)物体上升的速度。
(2)工人做功的功率。
(3)定滑轮的机械效率。(结果精确到 $ 0.1 \% $)

答案:
(1)物体上升的速度:
$v=\frac {s_{物}}{t}=\frac {3m}{6s}=0.5m/s$。
(2)定滑轮拉力端移动的距离:$s = h = 3m$,
工人做的总功:
$W_{总}=Fs=330N×3m=990J$,
工人做功的功率:$P=\frac {W_{总}}{t}=\frac {990J}{6s}=165W$。
(3)物体的重力:
$G = mg = 30kg×10N/kg = 300N$,
克服物体重力做的有用功:
$W_{有用}=Gh=300N×3m=900J$,
定滑轮的机械效率:$\eta=\frac {W_{有用}}{W_{总}}×100\%=\frac {900J}{990J}×100\% = 90.9\%$。
(1)物体上升的速度:
$v=\frac {s_{物}}{t}=\frac {3m}{6s}=0.5m/s$。
(2)定滑轮拉力端移动的距离:$s = h = 3m$,
工人做的总功:
$W_{总}=Fs=330N×3m=990J$,
工人做功的功率:$P=\frac {W_{总}}{t}=\frac {990J}{6s}=165W$。
(3)物体的重力:
$G = mg = 30kg×10N/kg = 300N$,
克服物体重力做的有用功:
$W_{有用}=Gh=300N×3m=900J$,
定滑轮的机械效率:$\eta=\frac {W_{有用}}{W_{总}}×100\%=\frac {900J}{990J}×100\% = 90.9\%$。
4. (2024 无锡期中)如图 Z-2-4 所示,塔式起重机上的滑轮组将质量为 600 kg 的物体提升 2 m,滑轮组的机械效率 80%,g 取 10 N/kg。
(1)求物体的重力。
(2)求滑轮组所做的有用功。
(3)若克服摩擦和钢丝绳重所做的功为 1000 J,求动滑轮的重力。

(1)求物体的重力。
(2)求滑轮组所做的有用功。
(3)若克服摩擦和钢丝绳重所做的功为 1000 J,求动滑轮的重力。

答案:
(1)物体的重力:
$G = mg = 600kg×10N/kg = 6000N$。
(2)使物体上升 2m 所做的有用功:
$W_{有用}=Gh=6000N×2m=12000J$。
(3)由$\eta=\frac {W_{有用}}{W_{总}}×100\%$可得,
拉力做的总功:
$W_{总}=\frac {W_{有用}}{\eta}=\frac {12000J}{80\%}=15000J$,
额外功:$W_{额外}=W_{总}-W_{有用}=15000J - 12000J = 3000J$,
克服动滑轮重力做的功:$W_{动}=W_{额外}-$活 12 全品学练考 物理 九年级上册 苏科
$W_{f}=3000J - 1000J = 2000J$,
动滑轮的重力:$G_{动}=\frac {W_{动}}{h}=\frac {2000J}{2m}=1000N$。
(1)物体的重力:
$G = mg = 600kg×10N/kg = 6000N$。
(2)使物体上升 2m 所做的有用功:
$W_{有用}=Gh=6000N×2m=12000J$。
(3)由$\eta=\frac {W_{有用}}{W_{总}}×100\%$可得,
拉力做的总功:
$W_{总}=\frac {W_{有用}}{\eta}=\frac {12000J}{80\%}=15000J$,
额外功:$W_{额外}=W_{总}-W_{有用}=15000J - 12000J = 3000J$,
克服动滑轮重力做的功:$W_{动}=W_{额外}-$活 12 全品学练考 物理 九年级上册 苏科
$W_{f}=3000J - 1000J = 2000J$,
动滑轮的重力:$G_{动}=\frac {W_{动}}{h}=\frac {2000J}{2m}=1000N$。
5. 建筑工人用如图 Z-2-5 甲所示的滑轮组运送建材上楼,每次运送量不定。滑轮组的机械效率随建材重力变化的图像如图乙所示。(不计绳重和摩擦,g 取 10 N/kg)
(1)动滑轮的重力是多大?
(2)若工人在 1 min 内将建材匀速竖直向上提升了 12 m,作用在钢绳上的拉力为 200 N,求拉力的功率。
(3)滑轮组的机械效率为 80%时,运送建材的重力是多大?
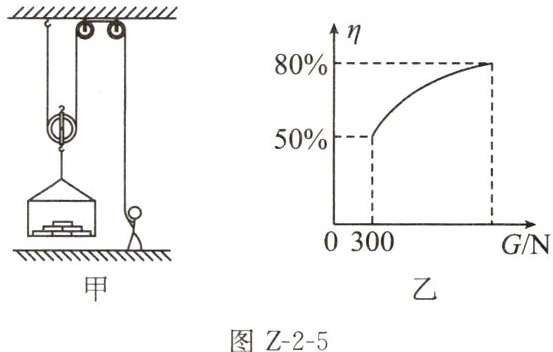
(1)动滑轮的重力是多大?
(2)若工人在 1 min 内将建材匀速竖直向上提升了 12 m,作用在钢绳上的拉力为 200 N,求拉力的功率。
(3)滑轮组的机械效率为 80%时,运送建材的重力是多大?

答案:
(1)由图乙可知,当建材重为$G_{1}=300N$时,
滑轮组的机械效率$\eta_{1}=50\%$,
由于摩擦及绳重忽略不计,
则滑轮组的机械效率:
$\eta=\frac {W_{有用}}{W_{总}}=\frac {W_{有用}}{W_{有用}+W_{额}}=\frac {Gh}{Gh+G_{动}h}=\frac {G}{G+G_{动}}$,
代入数据解得动滑轮的重力:$G_{动}=300N$。
(2)由图甲可知,该滑轮组中$n = 2$,1 min 内
绳子自由端移动的距离:
$s = nh = 2×12m = 24m$,
拉力做的功:
$W = Fs = 200N×24m = 4800J$;
拉力的功率:$P=\frac {W}{t}=\frac {4800J}{60s}=80W$。
(3)当滑轮组的机械效率为 80%时,根据
$\eta=\frac {G}{G+G_{动}}$可得,此时运送建材的重力:
$G'=\frac {\eta'G_{动}}{1-\eta'}=\frac {80\%×300N}{1 - 80\%}=1200N$。
(1)由图乙可知,当建材重为$G_{1}=300N$时,
滑轮组的机械效率$\eta_{1}=50\%$,
由于摩擦及绳重忽略不计,
则滑轮组的机械效率:
$\eta=\frac {W_{有用}}{W_{总}}=\frac {W_{有用}}{W_{有用}+W_{额}}=\frac {Gh}{Gh+G_{动}h}=\frac {G}{G+G_{动}}$,
代入数据解得动滑轮的重力:$G_{动}=300N$。
(2)由图甲可知,该滑轮组中$n = 2$,1 min 内
绳子自由端移动的距离:
$s = nh = 2×12m = 24m$,
拉力做的功:
$W = Fs = 200N×24m = 4800J$;
拉力的功率:$P=\frac {W}{t}=\frac {4800J}{60s}=80W$。
(3)当滑轮组的机械效率为 80%时,根据
$\eta=\frac {G}{G+G_{动}}$可得,此时运送建材的重力:
$G'=\frac {\eta'G_{动}}{1-\eta'}=\frac {80\%×300N}{1 - 80\%}=1200N$。
查看更多完整答案,请扫码查看


