《2025年全品学练考九年级物理上册苏科版江苏专版》

9. (2024南京栖霞区二模)用如图11-5-6所示的滑轮组将重为80N的物体匀速提升2m,拉力F为50N。此过程中有用功为____J,总功为____J,滑轮组的机械效率为____;根据已知条件,以下四个物理量:①动滑轮上升的高度,②动滑轮的重力,③额外功,④拉力的功率,能求出的有____和____(填序号)。

答案： 160　200　80%　①　③

10. (2024南京秦淮区校级月考)如图11-5-7所示,用竖直向上的力匀速拉动较长的杠杆,使重为18N的物体缓慢升高0.1m,拉力大小$F= 8N$,拉力移动的距离为0.25m。有用功为____J,杠杆的机械效率为____%,在缓缓拉起杠杆的过程中,拉力F的大小____(选填“增大”“减小”或“不变”)

答案： 1.8　90　不变

11. (2024连云港海州区二模)小丽用如图11-5-8所示装置使8N的重物以0.3m/s的速度匀速上升,所用拉力为5N,此时动滑轮的机械效率是____,拉力的功率是____W。若不计摩擦,动滑轮没能省一半力的主要原


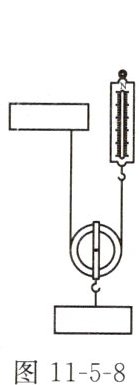
因是____。

答案： 80%　3　动滑轮有重力

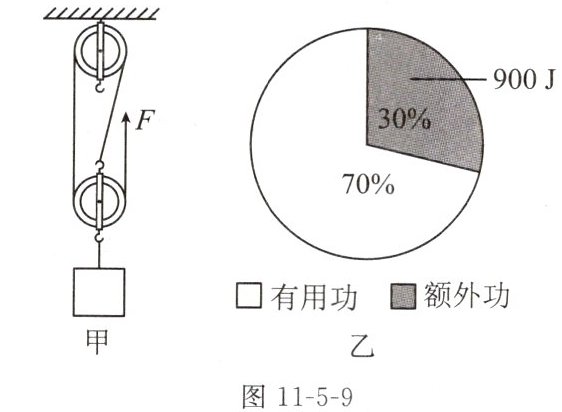
12. (2024连云港海州区二模)某同学用如图11-5-9甲所示的滑轮组提升重210N的物体,不计各种摩擦,提升过程中拉力做功的部分数据如图乙所示,则有用功为____J,所用拉力为____N,动滑轮的重力为____N。

答案： 2100　100　90

13. [教材变式题](2024苏州姑苏区校级月考)如图11-5-10所示塔式起重机上的滑轮组将重为$1.2×10^{4}N$的重物匀速吊起2m时,滑轮组的机械效率为80%,g取10N/kg。
(1)求提升重物做的有用功。
(2)求绳端的拉力。
(3)若动滑轮的质量为20kg,求克服摩擦和钢丝绳重所做的功。

答案：
(1)提升重物时需克服重物的重力做功，则所做的有用功:$W_{有用}=Gh=1.2×10^{4}N×2m=2.4×10^{4}J$。
(2)由图可知$n=3$，绳子自由端移动的距离:$s=nh=3×2m=6m$，
　　由$η=\frac {W_{有用}}{W_{总}}×100\% $可知，总功:$W_{总}=\frac {W_{有用}}{η}=\frac {2.4×10^{4}J}{80\% }=3×10^{4}J$；
　　由$W_{总}=Fs$可知，绳端的拉力:$F=\frac {W_{总}}{s}=\frac {3×10^{4}J}{6m}=5000N$。
(3)动滑轮的重力:$G_{动}=m_{动}g=20kg×10N/kg=200N$，
　　则克服动滑轮重力做的额外功:$W_{动}=G_{动}h=200N×2m=400J$，
　　额外功:$W_{额外}=W_{总}-W_{有用}=3×10^{4}J-2.4×10^{4}J=6000J$。
　　则克服摩擦和钢丝绳重所做的功:$W'=W_{额外}-W_{动}=6000J-400J=5600J$。

14. [开放探究]如图11-5-11所示,体重都为400N的小文和小志要把重100N的沙子运到三楼。方案一为小文的办法;学习了滑轮的知识后,小志利用滑轮设计了一个升降装置(方案二)。若不计绳重和摩擦,请结合题中信息回答下列问题:
(1)方案一中有用功和总功各是多少?
(2)方案二中动滑轮的机械效率是多少?(精确到0.1%)
(3)请你也设计一个升降装置,并说一说你设计的升降装置和方案二比有什么优点。

答案：

(1)方案一中，运沙子时做的有用功:$W_{有用}=G_{沙}h=100N×2×3m=600J$；
　　克服人的体重和桶的自重做的功为额外功，则$W_{额外}=(G_{桶}+G_{人})h=(20N+400N)×2×3m=2520J$；
　　总功:$W_{总}=W_{有用}+W_{额外}=600J+2520J=3120J$。
(2)方案二中，运沙子时做的有用功不变，克服动滑轮重和桶的自重做的功为额外功，
　　则$W_{额外}'=(G_{桶}+G_{动})h=(20N+10N)×2×3m=180J$；
　　所做的总功:$W_{总}'=W_{有用}+W_{额外}'=600J+180J=780J$；
　　则方案二中动滑轮的机械效率:$η=\frac {W_{有用}}{W_{总}'}×100\% =\frac {600J}{780J}×100\% =76.9\% $。
(3)如图所示
　　　　　
和方案二比不用克服动滑轮的自重做额外功，机械效率高，还可改变用力的方向。