《2025年轻松作业本九年级物理上册苏科版》

8. 杠杆受到两个拉力,忽略杠杆重。下列选项中,杠杆能保持水平静止且两个力臂相等的是()

答案： B

9. 如图所示,在轻质杠杆上吊一重物G,在一端施加一个始终与杠杆垂直的动力F,使杠杆缓慢地从OA转至水平位置OB,则在转动过程中,拉力F的大小将()

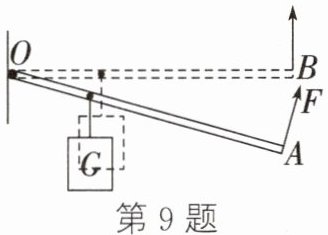
A. 逐渐变大
B. 先变大后变小
C. 保持不变
D. 先变小后变大

答案： A

10. 有一根重200N的木料AB水平放在地面上,一个人用50N的力就能抬起木料的A端,关于这根木料,下列说法正确的是()

A. 重心一定在木料中点
B. 重心离A端近
C. 要抬起B端至少用250N的力
D. 要抬起B端至少用150N的力

答案： D

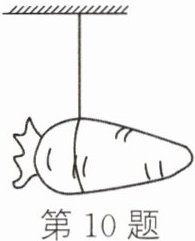
11. 如图,一根胡萝卜用细线悬挂后在水平位置平衡,如果从悬挂位置切开,则()
A. 细头较重
B. 细头较轻
C. 一样重
D. 无法判断

答案： B

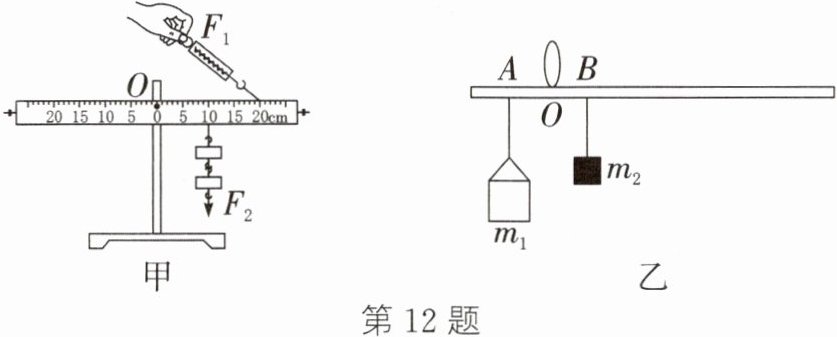
12. (2024·淮安)在“探究杠杆平衡条件”实验中：
(1)请在图甲中画出$F_{1}的力臂l_{1}$。
(2)$F_{2}的力臂l_{2}$为______cm。当$F_{2}$的大小为1N时,$F_{1}$竖直向上拉杠杆,仍使杠杆在水平位置平衡,$F_{1}= $______N。
(3)小明学过杠杆知识后自制了一根杆秤(自重不计),如图乙所示。要想增大杆秤的测量范围,你有哪些方法?______(写出一种方法即可)。小明猜想制作的杆秤刻度是均匀的,请你通过推理证实。______(写出推理过程,涉及的物理量用图中字母表示)。

答案：
（1）如图所示 （2）10.0 0.5 （3）①换用质量更大的秤砣 ②根据杠杆平衡条件可得：$ m_{1}g·OA=m_{2}g·OB $，则有：$ OB=\frac{OA}{m_{2}}·m_{1} $，因为 $ OA $ 和 $ m_{2} $ 均为定值，所以 $ OB $ 和 $ m_{1} $ 成正比，所以制作的杆秤刻度是均匀的

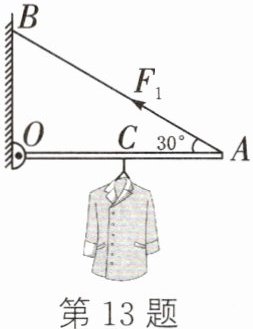
13. 如图所示是一款轻质悬挂式晾衣杆,OA为晾衣杆,AB为悬线,已知悬线能承受的最大拉力为20N,在悬线拉力$F_{1}$作用下,晾衣杆保持水平平衡。已知$OA= 1m$,$OC= 0.5m$,在C点悬挂衣物的质量为2kg。求：(g取10N/kg)
(1)悬挂衣物的挂钩对杠杆的作用力$F_{C}$。
(2)悬线拉力$F_{1}$的大小。

答案：
（1）衣物的重力 $ G=mg=2kg×10N/kg=20N $，悬挂衣物的挂钩对杠杆的作用力 $ F_{C}=G=20N $ （2）力臂是指从支点到力的作用线的垂直距离。画出 $ F_{1} $ 的力臂如图所示，由直角三角形的知识可知，拉力 $ F_{1} $ 的力臂 $ L_{1}=\frac{1}{2}OA=\frac{1}{2}×1m=0.5m $，杠杆水平平衡，则 $ F_{C} $ 的方向与杠杆垂直，其力臂等于 $ OC $ 的长（如图所示），即 $ L_{C}=OC=0.5m $，根据杠杆的平衡条件可得 $ F_{1}×L_{1}=F_{C}×L_{C} $，即：$ F_{1}×0.5m=20N×0.5m $，则 $ F_{1}=20N $