《2025年轻松作业本九年级物理上册苏科版》

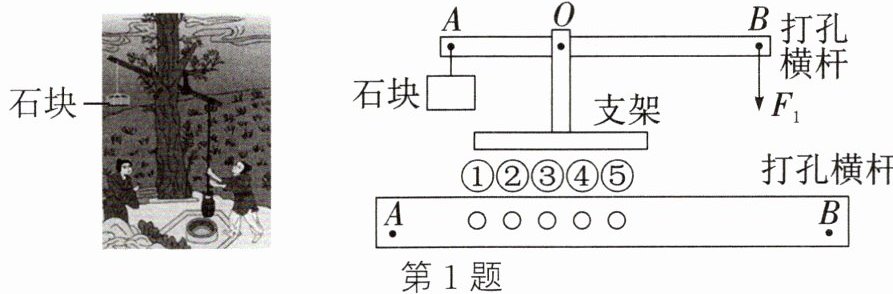
1. 小明仿照《天工开物》中记载的桔槔,制作如图所示的模型,以第③孔位置作为支点O,横杆水平静止时,B处所受动力为$F_{1}$,A处所受阻力为$F_{2}$。不计摩擦和横杆重力。
(1) 根据杠杆的平衡条件可知,此时$F_{1}$____$F_{2}(＞/= /＜)$,杠杆属于____(省力/费力/等臂)杠杆。
(2) 若石块和A、B点不变,$F_{1}$方向不变,支点可在如图五个孔的位置移动,横杆仍保持水平静止,支点O在____(①/②/④/⑤)孔的位置,$F_{1}$最小。

答案：
(1) ＜ 省力
(2) ①

2. 如图1,是我国古代的一种度量衡工具——杆秤,它承载着中华民族悠久的文化内涵。其木杆上的星星代表着衡量事物的标准和尺度,秤杆上从左向右起第一颗秤星,被称为“定盘星”,它是衡量事物的起始点。秤砣叫“权”,而秤杆则叫“衡”。在学习了杠杆平衡条件后,小明以“自制杆秤”为主题开展了一次跨学科实践活动。
(1) 如图2是小明用筷子、小纸杯、棉线和钩码制作的杆秤。把棉线系在“O”处,作为平纽；把小纸杯悬挂在“A”处,作为秤盘；用5g钩码作为秤砣。手提秤纽,移动秤砣使秤杆____平衡,此时秤砣所挂处的秤杆上标上“B”为定盘星,即为用杆秤读取质量示数大小的____线,同时避免了杆秤____对称量的干扰。在秤盘放置20g砝码作为重物,移动秤砣位置使秤杆恰好水平平衡,此时将连接秤砣的棉线在杆秤的位置标为20,然后在定盘星和20之间依次标上20等份的刻度。
(2) 如图3是小明制作的杆秤杠杆模型示意图。秤纽O点视为支点,秤杆和秤钩的重力为$G_{0}$,其重心在B点,秤砣在定盘星C点,秤砣的重力为$G_{1}$。当杆秤不挂重物时,$G_{1}\cdot OC$____$G_{0}\cdot OB(＞/= /＜)$。
(3) 为了验证杆秤的刻度是否均匀,当秤钩上挂上重物G,把秤砣移至距定盘星x处时,使杆秤在水平位置平衡,如图4。根据杠杆平衡条件,此时的表达式为$G\cdot OA+G_{0}\cdot OB= G_{1}\cdot$____(表达式使用图4中的相关条件),据此推理：由于秤砣质量$m_{1}$大小和秤纽位置是固定的,所以被称量物体的质量m与x成____比关系,杆秤上的刻度是均匀的。
(4) 小明想增大自制杆秤的测量范围,你的建议是____。
(5) 完成实验后,小明联想到了古人利用木棒搬动巨大的木料也用到了相同的原理。如图5是我们的祖先通过横杆、支架、石块等,将巨木的一端抬起,垫上圆木的劳动场景。结合制作杆秤的收获,小明认为：如果在人员有限的情况下,要抬起巨木,可以采用在不改变支点位置的情况下,让压横杆的人____支点移动等方法来实现。

答案：
(1) 水平 零刻度 重力
(2) =
(3) $(x + OC)$ 正
(4) 秤砣的质量不变，加大力臂的长度，那么可将提扭 O 向左移动
(5) 远离