第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. (真实情境)星期天的早晨小明登到山顶后可以采用两种路径下山,一种是从东面陡坡下山,需用时7min;另一种是从西面缓坡下山,需用时15min(设山下地面相平,不计摩擦)。则下列说法正确的是 (
A. 从东面下山,自身所受重力做功多一些
B. 从东面下山和从西面下山,自身所受重力做功一样多
C. 从西面下山,自身所受重力做功的功率大
D. 两种下山方式自身所受重力做功的快慢一样
B
)A. 从东面下山,自身所受重力做功多一些
B. 从东面下山和从西面下山,自身所受重力做功一样多
C. 从西面下山,自身所受重力做功的功率大
D. 两种下山方式自身所受重力做功的快慢一样
答案:
B
2. (模型建构)折叠床因隐形、节约空间等特点,备受欢迎。折叠床处于水平位置时的结构可简化成如图所示,折叠床可围绕O点转动,把床架和床垫看成一个整体,床两侧各装一根液压杆,液压杆连接了床架上B处和墙体上A处,利用液压杆可以在10s内收起床体,液压杆的拉力沿AB方向。已知床架上B处与O点的距离为0.5m,床体OC长度为2m,整个床体(包含床垫)质量约为100kg,整个床体厚度为0.2m,整个床体可视为质量分布均匀(g取10N/kg),则在收起床体过程中,下列说法正确的是 (
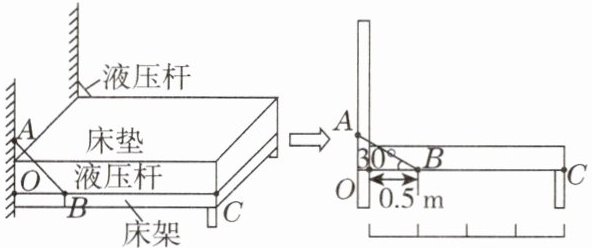
A. 液压杆和床架构成了省力杠杆
B. 克服床体重力做功为900J
C. 每根液压杆的拉力至少为4000N
D. 对床体做功的功率至少是80W
B
)
A. 液压杆和床架构成了省力杠杆
B. 克服床体重力做功为900J
C. 每根液压杆的拉力至少为4000N
D. 对床体做功的功率至少是80W
答案:
B
3. (图像分析)现定义人对机械施加的力与机械对重物施加的力的比值叫作机械效能K,用于比较不同机械的省力程度。用甲、乙两个滑轮(组)匀速提升不同重物,不计绳重和摩擦,经测算描绘出两滑轮(组)的机械效能K与物体重力的倒数$G^{-1}$的关系图像如图所示,两图线平行。则 (
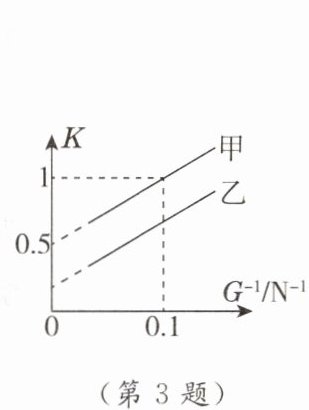
A. 甲为定滑轮,乙为动滑轮
B. 甲、乙滑轮(组)中动滑轮重相等
C. 提升相同重物时,乙滑轮(组)机械效率比甲小
D. 甲滑轮(组)提升20N重物时,机械效率为80%
C
)
A. 甲为定滑轮,乙为动滑轮
B. 甲、乙滑轮(组)中动滑轮重相等
C. 提升相同重物时,乙滑轮(组)机械效率比甲小
D. 甲滑轮(组)提升20N重物时,机械效率为80%
答案:
C 点拨: 不考虑绳重和摩擦, 若甲为定滑轮, 则 $ K=\frac{F}{G}=1 $, 由图可知甲的 $ K-G^{-1} $ 的图像不是过 1 平行于横轴的直线, 故 A 错误; 不考虑绳重和摩擦, 设 $ n_{1} 、 n_{2} $ 分别为甲、乙滑轮 (组) 承担动滑轮绳子的股数, 则 $ K_{\text {甲 }}=\frac{F_{\text {甲 }}}{G_{\text {甲 }}}=\frac{G_{\text {甲 }}+G_{\text {甲动 }}}{n_{1} G_{\text {甲 }}}=\frac{1}{n_{1}}+\frac{G_{\text {甲动 }}}{n_{1} G_{\text {甲 }}} $, 结合甲的图线可得 $ n_{1}=2 $, 把 $ G_{\text {甲 }}{ }^{-1}=0.1 \mathrm{~N}^{-1} $ 时 $ K=1 $ 代入上式解得 $ G_{\text {甲动 }}=10 \mathrm{~N} $, 同理, $ K_{\text {乙 }}=\frac{1}{n_{2}}+\frac{G_{\text {乙动 }}}{n_{2} G_{\text {乙 }}} $, 由图像可知 $ \frac{1}{n_{2}}<0.5 $, 所以 $ n_{2}>2 $, 即 $ n_{2}>n_{1} $, 甲、乙图线平行, 故 $ \frac{G_{\text {甲动 }}}{n_{1}}=\frac{G_{\text {乙动 }}}{n_{2}} $, 所以 $ G_{\text {甲动 }}< $ $ G_{\text {乙动 }} $, B 错误; 提升相同重物时, 设提升重物的重力为 $ G $, 机械效率 $ \eta_{\text {甲 }}=\frac{G}{G+G_{\text {甲动 }}} \times 100 \% 、 \eta_{\text {乙 }}=\frac{G}{G+G_{\text {乙动 }}} \times 100 \% $, 所以 $ \eta_{\text {甲 }}> $ $ \eta_{\text {乙 }} $, C 正确; 因 $ G_{\text {甲动 }}=10 \mathrm{~N} $, 所以用甲滑轮 (组) 提升 $ G^{\prime}=20 \mathrm{~N} $ 重物时的机械效率 $ \eta=\frac{G^{\prime}}{G^{\prime}+G_{\text {甲动 }}} \times 100 \%=\frac{20 \mathrm{~N}}{20 \mathrm{~N}+10 \mathrm{~N}} \times 100 \% \approx $ $ 66.7 \% $, D 错误。
4. 如图甲所示,滑轮组在竖直向上的拉力F作用下,将重为105N的物体匀速提起,其中动滑轮重40N,在5s时间内绳子自由端移动的距离为s= 3m。图乙是滑轮组工作时的拉力F与绳子自由端移动距离s的关系图,则图乙中阴影部分的面积表示的物理量是
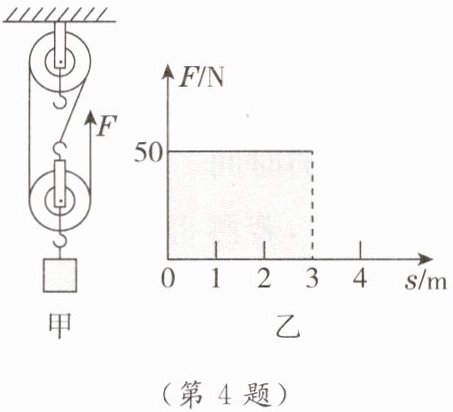
功
,拉力F做功的功率是30
W,该滑轮组提升此重物时的机械效率为70%
。
答案:
功; 30 ; 70 %
5. (体育)小艾妈妈正使用一款可调节阻力的坐姿划船机进行锻炼,她每次划船运动的距离相同。划船机还可通过调节装置设定不同的阻力级别。当小艾妈妈在某个阻力级别以稳定的节奏划船时,显示器上的参数如图,在这1min内妈妈划船所做的功是
9000
J,阻力是300
N。若教练将阻力大小调节为原来的2倍,并建议小艾妈妈将功率保持在100W,则小艾妈妈1min内划船的次数变为10
次。
答案:
9 000 ; 300 ; 10
6. (新情境实验)风车是利用风力做功的装置。小明带领物理兴趣小组制作了一架小风车,想粗略测定风车在一定风速下做功的功率,利用如图实验装置进行实验:

①将叶片安装在风车底座上,把线的一端固定在风车转轴上,另一端系上钩码;
②在风车正前方1m处放置电风扇,将电风扇的风速调到1挡位,用秒表记录提升钩码到A点所需的时间。
(1)实验时,若测得钩码上升到A点的高度h、所用的时间t、钩码的质量m,则风车做功的功率P= ____
(2)实验交流时,兴趣小组的同学又提出了“风车做功的功率与风速有什么关系”的问题,于是同学们进行了探究,并将实验收集到的数据记录在下表中(注:电风扇挡位越高,风速越大)。
|电风扇挡位|钩码的质量/g|提升钩码到A点的时间/s|
|----|----|----|
|1|50|15|
|2|50|13|
|3|50|10|
①实验中,通过测量____
②由表格数据可初步得出:在其他条件相同时,风速越大,风车的输出功率____
(3)兴趣小组在交流评估时有同学提出“上述结论是否符合普遍规律呢”的问题,小明从网上查到风速与风力发电机的输出功率的关系如下表:
|风速$/(m·s⁻^1)$|4|6|8|10|12|14|16|18|20|
|----|----|----|----|----|----|----|----|----|----|
|输出功率/kW|0|75|200|360|540|740|730|650|550|
①小明由表格数据得出:风速为14m/s时风力发电机的输出功率最大。你认为他的判断是____
②根据表中数据分析,随着风速的增大,给风电场发电带来的经济效益____

①将叶片安装在风车底座上,把线的一端固定在风车转轴上,另一端系上钩码;
②在风车正前方1m处放置电风扇,将电风扇的风速调到1挡位,用秒表记录提升钩码到A点所需的时间。
(1)实验时,若测得钩码上升到A点的高度h、所用的时间t、钩码的质量m,则风车做功的功率P= ____
$\frac{mgh}{t}$
(用所给物理量符号表示)。(2)实验交流时,兴趣小组的同学又提出了“风车做功的功率与风速有什么关系”的问题,于是同学们进行了探究,并将实验收集到的数据记录在下表中(注:电风扇挡位越高,风速越大)。
|电风扇挡位|钩码的质量/g|提升钩码到A点的时间/s|
|----|----|----|
|1|50|15|
|2|50|13|
|3|50|10|
①实验中,通过测量____
提升钩码到A点的时间
来比较风车输出功率的大小。②由表格数据可初步得出:在其他条件相同时,风速越大,风车的输出功率____
越大
(选填“越大”或“越小”)。(3)兴趣小组在交流评估时有同学提出“上述结论是否符合普遍规律呢”的问题,小明从网上查到风速与风力发电机的输出功率的关系如下表:
|风速$/(m·s⁻^1)$|4|6|8|10|12|14|16|18|20|
|----|----|----|----|----|----|----|----|----|----|
|输出功率/kW|0|75|200|360|540|740|730|650|550|
①小明由表格数据得出:风速为14m/s时风力发电机的输出功率最大。你认为他的判断是____
不准确
(选填“准确”或“不准确”)的,理由是____没有仔细探究风速在14m/s附近时风力发电机输出功率的变化情况
。②根据表中数据分析,随着风速的增大,给风电场发电带来的经济效益____
先变大后变小
(选填“变大”“变小”“先变大后变小”或“先变小后变大”)。
答案:
(1) $ \frac{m g h}{t} $
(2)
(1)提升钩码到 $ A $ 点的时间
(2)越大
(3)
(1)不准确; 没有仔细探究风速在 $ 14 \mathrm{~m} / \mathrm{s} $ 附近时风力发电机输出功率的变化情况
(2)先变大后变小
(1) $ \frac{m g h}{t} $
(2)
(1)提升钩码到 $ A $ 点的时间
(2)越大
(3)
(1)不准确; 没有仔细探究风速在 $ 14 \mathrm{~m} / \mathrm{s} $ 附近时风力发电机输出功率的变化情况
(2)先变大后变小
查看更多完整答案,请扫码查看


