《2025年点拨训练九年级物理上册苏科版》

5. 港珠澳大桥是中国第一条集桥、双人工岛、隧道为一体的跨海通道,其中长约5600m的沉管隧道通过引桥与人工岛路面相连,引桥长约1000m,竖直高度为40m,其简化图如图所示。重$5×10^4N$的汽车(大小不计)在沉管隧道中以90km/h的速度匀速行驶,所受阻力为其重力的1/20,行驶到引桥底端后开始匀速爬升,其功率增大到90kW,耗时45s到达人工岛路面,求：
(1)汽车完全通过沉管隧道需要的时间为224s。
(2)汽车在沉管隧道中行驶时牵引力所做的功为1.4×10⁷J。
(3)汽车在引桥上所受阻力的大小为2050N。(已知牵引力所做的功一部分用于克服重力,剩下的用于克服阻力)
(4)引桥对于该汽车的机械效率为49.4%。(百分号前保留一位小数)

答案： 解:
(1) 沉管隧道中汽车速度 $ v = 90 \, \text{km/h} = 25 \, \text{m/s} $
则汽车完全通过沉管隧道需要的时间 $ t = \frac{s_{1}}{v} = \frac{5600 \, \text{m}}{25 \, \text{m/s}} = 224 \, \text{s} $
(2) 汽车所受阻力大小 $ f = \frac{1}{20}G = \frac{1}{20} \times 5 \times 10^{4} \, \text{N} = 2500 \, \text{N} $
因为汽车做匀速直线运动, 所以汽车所受牵引力 $ F = f = 2500 \, \text{N} $
汽车在沉管隧道中行驶时牵引力做的功 $ W_{1} = Fs_{1} = 2500 \, \text{N} \times 5600 \, \text{m} = 1.4 \times 10^{7} \, \text{J} $
(3) 汽车在引桥上行驶时, 功率 $ P = 90 \, \text{kW} = 9 \times 10^{4} \, \text{W} $
根据 $ P = \frac{W}{t} $ 可得, 牵引力所做的功 $ W_{\text{牵}} = Pt' = 9 \times 10^{4} \, \text{W} \times 45 \, \text{s} = 4.05 \times 10^{6} \, \text{J} $
重力做功 $ W_{\text{重}} = Gh = 5 \times 10^{4} \, \text{N} \times 40 \, \text{m} = 2 \times 10^{6} \, \text{J} $
阻力做功 $ W_{2} = W_{\text{牵}} - W_{\text{重}} = 4.05 \times 10^{6} \, \text{J} - 2 \times 10^{6} \, \text{J} = 2.05 \times 10^{6} \, \text{J} $
汽车在引桥上所受阻力大小 $ f' = \frac{W_{2}}{s_{2}} = \frac{2.05 \times 10^{6} \, \text{J}}{1000 \, \text{m}} = 2050 \, \text{N} $
(4) 汽车从引桥底端到顶端, 所做的有用功为克服重力做的功, 即 $ W_{\text{有用}} = W_{\text{重}} = 2 \times 10^{6} \, \text{J} $
总功为牵引力做的功, 即 $ W_{\text{总}} = W_{\text{牵}} = 4.05 \times 10^{6} \, \text{J} $
引桥对于该汽车的机械效率 $ \eta = \frac{W_{\text{有用}}}{W_{\text{总}}} \times 100\% = \frac{2 \times 10^{6} \, \text{J}}{4.05 \times 10^{6} \, \text{J}} \times 100\% \approx 49.4\% $

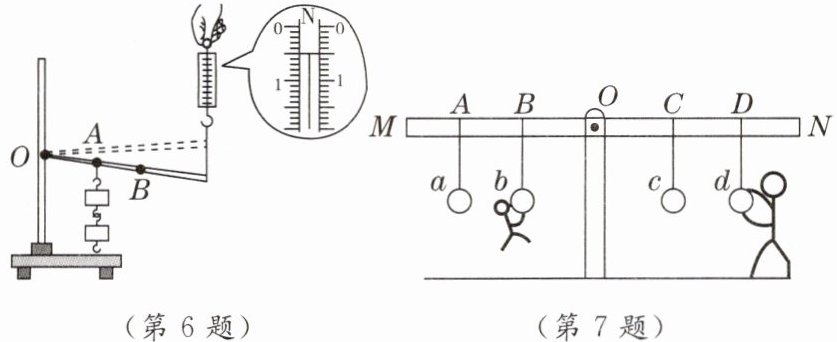
6. [2024·常州期中]用如图所示的实验装置测量杠杆的机械效率,将杠杆拉至图中虚线位置,实验时弹簧测力计的示数始终如图所示,若钩码总重G为1.0N,钩码上升高度h为0.1m,弹簧测力计上升高度s为0.3m。则弹簧测力计对杠杆做功0.15J,杠杆的机械效率为66.7%(百分号前保留一位小数)。若把钩码移至B点,用同样大小的力把钩码提升相同的高度,机械效率变大(选填“变大”“变小”或“不变”)。

答案： $ 0.15 $；$ 66.7\% $；变大

7. (跨学科实践)如图所示,杠杆MON可绕O点转动,a、b、c、d是四个供人娱乐的吊环,2OB= OD,父子俩在吊环上做游戏,质量为40kg的儿子吊在b环上,父亲站在地面上竖直向下拉着d环。(g取10N/kg)
(1)若不计杠杆和吊环的重力以及转轴间的摩擦力,为使杠杆在水平位置平衡,父亲要用多大的力拉吊环d？
(2)若父亲实际施加竖直向下的拉力为250N,在4s内将儿子匀速拉高0.4m,父亲做了多少功？
(3)父亲提升儿子的过程中,该器材的机械效率为多少？

答案： 解:
(1) 设父亲用的力为 $ F_{1} $，由题知 $ OB = \frac{1}{2}OD $
根据杠杆平衡条件 $ F_{1}l_{1} = F_{2}l_{2} $ 可得, $ F_{1} \times OD = mg \times OB $，则
$ F_{1} = \frac{40 \, \text{kg} \times 10 \, \text{N/kg} \times \frac{1}{2}OD}{OD} = 200 \, \text{N} $
(2) 根据相似三角形的性质可得 $ \frac{s_{\text{父亲}}}{s_{\text{儿子}}} = \frac{OD}{OB} = 2 $
父亲拉力移动的距离 $ s_{\text{父亲}} = 2s_{\text{儿子}} = 2 \times 0.4 \, \text{m} = 0.8 \, \text{m} $
父亲做功 $ W_{\text{总}} = F_{1}'s_{\text{父亲}} = 250 \, \text{N} \times 0.8 \, \text{m} = 200 \, \text{J} $
(3) 父亲用该器材提升儿子的过程中, 所做的有用功
$ W_{\text{有用}} = Gh = mgs_{\text{儿子}} = 40 \, \text{kg} \times 10 \, \text{N/kg} \times 0.4 \, \text{m} = 160 \, \text{J} $
该器材的机械效率
$ \eta = \frac{W_{\text{有用}}}{W_{\text{总}}} \times 100\% = \frac{160 \, \text{J}}{200 \, \text{J}} \times 100\% = 80\% $