2025年奔跑吧少年八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. 证明“若$∠A+∠B= 180^{\circ },∠C+∠D= 180^{\circ },$ $∠A= ∠C$,则$∠B= ∠D$”是真命题,以下是打乱的推理过程:
①因为$∠A= ∠C$(已知);
②因为$∠A+∠B= 180^{\circ },∠C+∠D= 180^{\circ }$(已知);
③所以$∠B= 180^{\circ }-∠A,∠D= 180^{\circ }-∠C$(等式的基本性质);
④所以$∠B= ∠D$(等量代换);
⑤所以$∠B= 180^{\circ }-∠C$(等量代换)。
正确的顺序是 (
A. ①→③→②→⑤→④
B. ②→③→⑤→①→④
C. ②→③→①→⑤→④
D. ②→⑤→①→③→④
①因为$∠A= ∠C$(已知);
②因为$∠A+∠B= 180^{\circ },∠C+∠D= 180^{\circ }$(已知);
③所以$∠B= 180^{\circ }-∠A,∠D= 180^{\circ }-∠C$(等式的基本性质);
④所以$∠B= ∠D$(等量代换);
⑤所以$∠B= 180^{\circ }-∠C$(等量代换)。
正确的顺序是 (
C
)A. ①→③→②→⑤→④
B. ②→③→⑤→①→④
C. ②→③→①→⑤→④
D. ②→⑤→①→③→④
答案:
C
10. 某密码锁的密码是一个三位数,小亮说:“它是 254。”小明说:“它是 964。”小强说:“它是 357。”最后由小颖揭秘说:“你们每人都只猜对了不同数位的一个数字。”这个密码锁的密码是
267
。
答案:
267
11. 把下面的证明过程补充完整。
如图,在$△ABO$中,$∠AOB= 90^{\circ },DE⊥AO$于点 E,$∠CFB= ∠EDO$。求证:$CF// DO$。
证明:因为$DE⊥AO$(已知),
所以
又因为$∠AOB= 90^{\circ }$(已知),
所以$∠AOB= $
所以
所以$∠EDO= $
又因为$∠CFB= ∠EDO$(已知),
所以$∠CFB= $
所以$CF// DO$(
如图,在$△ABO$中,$∠AOB= 90^{\circ },DE⊥AO$于点 E,$∠CFB= ∠EDO$。求证:$CF// DO$。
证明:因为$DE⊥AO$(已知),
所以
∠AED
$=90^{\circ }$(垂直的定义)。又因为$∠AOB= 90^{\circ }$(已知),
所以$∠AOB= $
∠AED
(等量代换),所以
DE//OB
(同位角相等,两直线平行
),所以$∠EDO= $
∠BOD
(两直线平行,内错角相等
)。又因为$∠CFB= ∠EDO$(已知),
所以$∠CFB= $
∠BOD
(等量代换),所以$CF// DO$(
同位角相等,两直线平行
)。
答案:
因为$DE⊥AO$(已知),所以$∠AED =90^{\circ }$(垂直的定义)。又因为$∠AOB=90^{\circ }$(已知),所以$∠AOB=∠AED$(等量代换),所以$DE// OB$(同位角相等,两直线平行),所以$∠EDO=∠BOD$(两直线平行,内错角相等)。又因为$∠CFB=∠EDO$(已知),所以$∠CFB=∠BOD$(等量代换),所以$CF// DO$(同位角相等,两直线平行)。
12. 如图,已知$AD⊥BC$于点 D,点 E 在 BA 的延长线上,$EG⊥BC$于点 G,交 AC 于点 F,$∠E$ $=∠1$。求证:AD 平分$∠BAC$。
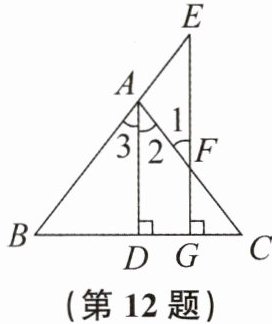

答案:
因为$\angle 2=\angle 3$,所以$AD$平分$\angle BAC$(角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线)。
13. 如图,已知 AM 平分$∠BAC,∠CAM= ∠CMA$。
(1)如图①,点 E 在射线 AB 上,点 F 在线段 CM 上。若$∠AEF= ∠C$,求证:$EF// AC$。
(2)如图②,将(1)中的点 F 移动到线段 CM 的延长线上,使$EF// AC$。若$∠CAM= 3∠MEF= 57^{\circ },请直接写出∠AME$的度数。
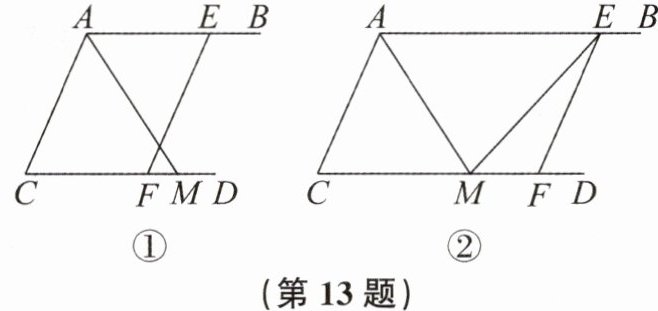
(1) 证明过程如上述解析;(2)
(1)如图①,点 E 在射线 AB 上,点 F 在线段 CM 上。若$∠AEF= ∠C$,求证:$EF// AC$。
(2)如图②,将(1)中的点 F 移动到线段 CM 的延长线上,使$EF// AC$。若$∠CAM= 3∠MEF= 57^{\circ },请直接写出∠AME$的度数。

(1) 证明过程如上述解析;(2)
38°
答案:
$(1)$ 证明过程如上述解析;$(2)$$\boldsymbol{38^{\circ}}$
查看更多完整答案,请扫码查看


