2025年奔跑吧少年八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列不等式组中,属于一元一次不等式组的是(
A. $\left\{ \begin{array} { l } { x + 3 > 2, } \\ { \frac { 1 } { x } + 2 < 5 } \end{array} \right.$
B. $\left\{ \begin{array} { l } { x + y > 4, } \\ { x - y < 6 } \end{array} \right.$
C. $\left\{ \begin{array} { l } { x + 4 \geq - 3, } \\ { 6 < 12 } \end{array} \right.$
D. $\left\{ \begin{array} { l } { x - 6 > - 2, } \\ { x + 1 < 8 } \end{array} \right.$
D
)A. $\left\{ \begin{array} { l } { x + 3 > 2, } \\ { \frac { 1 } { x } + 2 < 5 } \end{array} \right.$
B. $\left\{ \begin{array} { l } { x + y > 4, } \\ { x - y < 6 } \end{array} \right.$
C. $\left\{ \begin{array} { l } { x + 4 \geq - 3, } \\ { 6 < 12 } \end{array} \right.$
D. $\left\{ \begin{array} { l } { x - 6 > - 2, } \\ { x + 1 < 8 } \end{array} \right.$
答案:
D
2. 一个一元一次不等式组的解集在数轴上表示如图,则此不等式组的解集是(
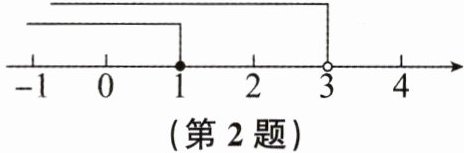
A. $x \leq 1$
B. $x < 3$
C. $1 \leq x < 3$
D. $x < 1$
A
)
A. $x \leq 1$
B. $x < 3$
C. $1 \leq x < 3$
D. $x < 1$
答案:
A
3. 不等式组$\left\{ \begin{array} { l } { - 2 x \leq 4, } \\ { x < 1 } \end{array} \right.$的解集在数轴上表示正确的是(

A
)
答案:
A
4. 下列四个数中,是不等式组$\left\{ \begin{array} { l } { 3 x - 6 < 0, } \\ { 3 + x > 3 } \end{array} \right.$的解的为(
A. $- 1$
B. $0$
C. $1$
D. $2$
C
)A. $- 1$
B. $0$
C. $1$
D. $2$
答案:
C
5. 下列不等式组中,解集为$- 1 \leq x < 5$的是(
A. $\left\{ \begin{array} { l } { x \geq - 1, } \\ { x > 5 } \end{array} \right.$
B. $\left\{ \begin{array} { l } { x - 5 > 0, } \\ { x + 1 \leq 0 } \end{array} \right.$
C. $\left\{ \begin{array} { l } { x - 5 < 0, } \\ { x + 1 \geq 0 } \end{array} \right.$
D. $\left\{ \begin{array} { l } { x + 5 < 0, } \\ { x + 1 \leq 0 } \end{array} \right.$
C
)A. $\left\{ \begin{array} { l } { x \geq - 1, } \\ { x > 5 } \end{array} \right.$
B. $\left\{ \begin{array} { l } { x - 5 > 0, } \\ { x + 1 \leq 0 } \end{array} \right.$
C. $\left\{ \begin{array} { l } { x - 5 < 0, } \\ { x + 1 \geq 0 } \end{array} \right.$
D. $\left\{ \begin{array} { l } { x + 5 < 0, } \\ { x + 1 \leq 0 } \end{array} \right.$
答案:
C
6. 不等式组$\left\{ \begin{array} { l } { x + 2 < 4, } \\ { - \frac { 1 } { 3 } x + 1 \leq 2 } \end{array} \right.$的解集为
$-3\leqslant x<2$
。
答案:
$-3\leqslant x<2$
7. 如图,点$C位于点A$,$B$之间(点$C不与点A$,$B$重合),点$C表示1 - 2 x$,则$x$的取值范围是
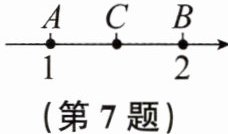
$-\frac{1}{2}<x<0$
。
答案:
$-\frac{1}{2}<x<0$
8. 解不等式组$\left\{ \begin{array} { l } { x + 1 \geq 2 ①, } \\ { 5 x \leq 4 x + 3 ②. } \end{array} \right.$请结合题意填空,完成下列问题。
(1)解不等式①,得
(2)解不等式②,得
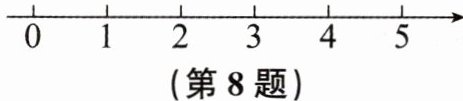
(3)把不等式①和②的解集在数轴(如图)上表示出来。
(4)原不等式组的解集为
(1)解不等式①,得
$x\geqslant 1$
。(2)解不等式②,得
$x\leqslant 3$
。(3)把不等式①和②的解集在数轴(如图)上表示出来。
(4)原不等式组的解集为
$1\leqslant x\leqslant 3$
。
答案:
(1)$x\geqslant 1$
(2)$x\leqslant 3$
(3)略
(4)$1\leqslant x\leqslant 3$
(1)$x\geqslant 1$
(2)$x\leqslant 3$
(3)略
(4)$1\leqslant x\leqslant 3$
9. 解不等式组,并把解集表示在数轴上。
(1)$\left\{ \begin{array} { l } { 2 x - 7 < 0, } \\ { 3 x + 4 > 0. } \end{array} \right.$
(2)$\left\{ \begin{array} { l } { x + 1 < 0, } \\ { 2 ( x - 1 ) \geq x + 2. } \end{array} \right.$
(3)$\left\{ \begin{array} { l } { 3 x - 2 < x, } \\ { \frac { 1 } { 3 } x < - 2. } \end{array} \right.$
(4)$\left\{ \begin{array} { l } { 2 ( x - 1 ) + 1 > - 3, } \\ { x - 1 \leq \frac { 1 + x } { 3 }. } \end{array} \right.$
(1)$\left\{ \begin{array} { l } { 2 x - 7 < 0, } \\ { 3 x + 4 > 0. } \end{array} \right.$
(2)$\left\{ \begin{array} { l } { x + 1 < 0, } \\ { 2 ( x - 1 ) \geq x + 2. } \end{array} \right.$
(3)$\left\{ \begin{array} { l } { 3 x - 2 < x, } \\ { \frac { 1 } { 3 } x < - 2. } \end{array} \right.$
(4)$\left\{ \begin{array} { l } { 2 ( x - 1 ) + 1 > - 3, } \\ { x - 1 \leq \frac { 1 + x } { 3 }. } \end{array} \right.$
答案:
$(1)$ 解不等式组$\begin{cases}2x - 7 \lt 0 \\3x + 4 \gt 0 \end{cases}$
- 解不等式$2x - 7 \lt 0$:
移项可得$2x\lt 7$,两边同时除以$2$,解得$x\lt \frac{7}{2}$。
- 解不等式$3x + 4 \gt 0$:
移项可得$3x\gt - 4$,两边同时除以$3$,解得$x\gt -\frac{4}{3}$。
所以不等式组的解集为$-\frac{4}{3} \lt x \lt \frac{7}{2}$。
$(2)$ 解不等式组$\begin{cases}x + 1 \lt 0 \\2(x - 1) \geq x + 2 \end{cases}$
- 解不等式$x + 1 \lt 0$:
移项可得$x\lt - 1$。
- 解不等式$2(x - 1) \geq x + 2$:
去括号得$2x-2\geq x + 2$,移项可得$2x-x\geq 2 + 2$,解得$x\geq 4$。
因为$x\lt - 1$与$x\geq 4$没有公共部分,所以此不等式组无解。
$(3)$ 解不等式组$\begin{cases}3x - 2 \lt x \\frac{1}{3}x \lt - 2 \end{cases}$
- 解不等式$3x - 2 \lt x$:
移项可得$3x-x\lt 2$,即$2x\lt 2$,两边同时除以$2$,解得$x\lt 1$。
- 解不等式$\frac{1}{3}x \lt - 2$:
两边同时乘以$3$,解得$x\lt - 6$。
所以不等式组的解集为$x\lt - 6$。
$(4)$ 解不等式组$\begin{cases}2(x - 1)+1 \gt - 3 \\x - 1 \leq \frac{1 + x}{3} \end{cases}$
- 解不等式$2(x - 1)+1 \gt - 3$:
去括号得$2x-2 + 1\gt - 3$,即$2x-1\gt - 3$,移项可得$2x\gt - 3 + 1$,$2x\gt - 2$,两边同时除以$2$,解得$x\gt - 1$。
- 解不等式$x - 1 \leq \frac{1 + x}{3}$:
两边同时乘以$3$得$3x-3\leq 1 + x$,移项可得$3x-x\leq 1 + 3$,$2x\leq 4$,两边同时除以$2$,解得$x\leq 2$。
所以不等式组的解集为$-1 \lt x \leq 2$。
数轴表示略(按照各解集在数轴上表示出范围即可,注意空心点和实心点的区别)。
综上,$(1)$解集为$-\frac{4}{3} \lt x \lt \frac{7}{2}$;$(2)$无解;$(3)$解集为$x\lt - 6$;$(4)$解集为$-1 \lt x \leq 2$。
- 解不等式$2x - 7 \lt 0$:
移项可得$2x\lt 7$,两边同时除以$2$,解得$x\lt \frac{7}{2}$。
- 解不等式$3x + 4 \gt 0$:
移项可得$3x\gt - 4$,两边同时除以$3$,解得$x\gt -\frac{4}{3}$。
所以不等式组的解集为$-\frac{4}{3} \lt x \lt \frac{7}{2}$。
$(2)$ 解不等式组$\begin{cases}x + 1 \lt 0 \\2(x - 1) \geq x + 2 \end{cases}$
- 解不等式$x + 1 \lt 0$:
移项可得$x\lt - 1$。
- 解不等式$2(x - 1) \geq x + 2$:
去括号得$2x-2\geq x + 2$,移项可得$2x-x\geq 2 + 2$,解得$x\geq 4$。
因为$x\lt - 1$与$x\geq 4$没有公共部分,所以此不等式组无解。
$(3)$ 解不等式组$\begin{cases}3x - 2 \lt x \\frac{1}{3}x \lt - 2 \end{cases}$
- 解不等式$3x - 2 \lt x$:
移项可得$3x-x\lt 2$,即$2x\lt 2$,两边同时除以$2$,解得$x\lt 1$。
- 解不等式$\frac{1}{3}x \lt - 2$:
两边同时乘以$3$,解得$x\lt - 6$。
所以不等式组的解集为$x\lt - 6$。
$(4)$ 解不等式组$\begin{cases}2(x - 1)+1 \gt - 3 \\x - 1 \leq \frac{1 + x}{3} \end{cases}$
- 解不等式$2(x - 1)+1 \gt - 3$:
去括号得$2x-2 + 1\gt - 3$,即$2x-1\gt - 3$,移项可得$2x\gt - 3 + 1$,$2x\gt - 2$,两边同时除以$2$,解得$x\gt - 1$。
- 解不等式$x - 1 \leq \frac{1 + x}{3}$:
两边同时乘以$3$得$3x-3\leq 1 + x$,移项可得$3x-x\leq 1 + 3$,$2x\leq 4$,两边同时除以$2$,解得$x\leq 2$。
所以不等式组的解集为$-1 \lt x \leq 2$。
数轴表示略(按照各解集在数轴上表示出范围即可,注意空心点和实心点的区别)。
综上,$(1)$解集为$-\frac{4}{3} \lt x \lt \frac{7}{2}$;$(2)$无解;$(3)$解集为$x\lt - 6$;$(4)$解集为$-1 \lt x \leq 2$。
查看更多完整答案,请扫码查看


