2025年奔跑吧少年八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列能作为证明依据的是 (
A. 已知条件
B. 定义和基本事实
C. 定理和推论
D. 以上三项都可以
D
)A. 已知条件
B. 定义和基本事实
C. 定理和推论
D. 以上三项都可以
答案:
D
2. 如果$∠1+∠2= 90^{\circ },∠1= ∠3$,那么$∠2+∠3= 90^{\circ }$,推理依据是 (
A. 同角的余角相等
B. 等角的余角相等
C. 等量代换
D. 余角的定义
C
)A. 同角的余角相等
B. 等角的余角相等
C. 等量代换
D. 余角的定义
答案:
C
3. 如图,点 E 在 AC 的延长线上。若想证明$AB// $ CD,则需要的条件可以是 (
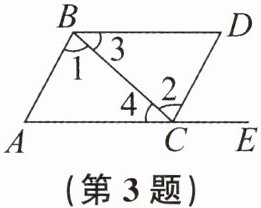
A. $∠1= ∠2$
B. $∠3= ∠4$
C. $∠D= ∠DCE$
D. $∠D+∠ACD= 180^{\circ }$
A
)
A. $∠1= ∠2$
B. $∠3= ∠4$
C. $∠D= ∠DCE$
D. $∠D+∠ACD= 180^{\circ }$
答案:
A
4. 如图,将一把含有$30^{\circ }$角的三角尺的两个顶点放在一张长方形纸片的对边上。如果$∠2= 34^{\circ }$,那么$∠1$的度数为 (
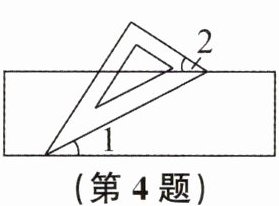
A. $24^{\circ }$
B. $25^{\circ }$
C. $26^{\circ }$
D. $27^{\circ }$
C
)
A. $24^{\circ }$
B. $25^{\circ }$
C. $26^{\circ }$
D. $27^{\circ }$
答案:
C
5. 如图所示为过直线外一点作已知直线的平行线的一种方法,其依据是“

同位
角相等,两直线平行”。
答案:
同位
6. 如图,若$∠BAF= 45^{\circ },∠ACE= 135^{\circ },CE⊥$ CD,则 CD 与 AB____
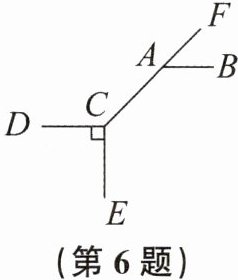
是
(填“是”或“不是”)相互平行的。
答案:
是
7. 如图,已知$AB// CD$,EM, FN 分别平分$∠BEF$和 $∠CFE$。求证:$EM// FN$。请把过程填写完整。
证明:因为$AB// CD$(已知),
所以$∠BEF= ∠CFE$(
因为 EM,FN 分别平分$∠BEF和∠CFE$(已知),
所以$∠MEF= $
所以$∠MEF= $
所以$EM// FN$(
证明:因为$AB// CD$(已知),
所以$∠BEF= ∠CFE$(
两直线平行,内错角相等
)。因为 EM,FN 分别平分$∠BEF和∠CFE$(已知),
所以$∠MEF= $
$\frac{1}{2}∠BEF$
,$∠NFE$
$=\frac {1}{2}∠CFE$(角平分线的定义
),所以$∠MEF= $
$∠NFE$
(等量代换
),所以$EM// FN$(
内错角相等,两直线平行
)。
答案:
两直线平行,内错角相等 $\frac{1}{2}∠BEF$ $∠NFE$ 角平分线的定义 $∠NFE$ 等量代换 内错角相等,两直线平行
8. 如图,已知$AC// EF,∠1+∠2= 180^{\circ }$。求证:$∠FAB= ∠CDB$。
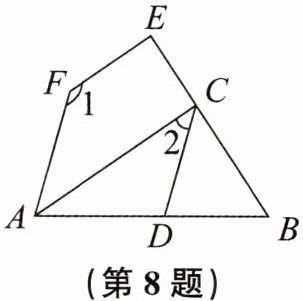
证明:

证明:
证明过程如上述解析,可证得$\angle FAB = \angle CDB$。
答案:
证明过程如上述解析,可证得$\angle FAB = \angle CDB$。
查看更多完整答案,请扫码查看


