《2025年奔跑吧少年八年级数学上册浙教版》

1. 命题“若 $ m = - n $,则 $ m ^ { 2 } = n ^ { 2 } $”的逆命题是(D)
A. 若 $ m ^ { 2 } = n ^ { 2 } $,则 $ m \neq - n $
B. 若 $ m = - n $,则 $ m ^ { 2 } \neq n ^ { 2 } $
C. 若 $ m ^ { 2 } \neq n ^ { 2 } $,则 $ m = n $
D. 若 $ m ^ { 2 } = n ^ { 2 } $,则 $ m = - n $

答案： D

2. 下列说法中,错误的是(C)
A. 任何一个命题都有逆命题
B. 一个定理不一定有逆定理
C. 真命题的逆命题一定是真命题
D. 假命题的逆命题可能是真命题

答案： C

3. 下列命题中,其逆命题是真命题的为(B)
A. 如果 $ a ＞ 0 $,$ b ＞ 0 $,那么 $ a b ＞ 0 $
B. 能够完全重合的两个三角形全等
C. 能被 9 整除的数,也能被 3 整除
D. 全等三角形的周长相等

答案： B

4. 下列选项中,可以用来证明命题“若 $ a ＞ 2 $,则 $ a ^ { 2 } ＞ 4 $”的逆命题是假命题的反例是(A)
A. $ a = - 3 $
B. $ a = - 2 $
C. $ a = 5 $
D. $ a = 2 $

答案： A

5. 下列定理中,有逆定理的是(D)
A. 四边形的外角和等于 $ 360 ^ { \circ } $
B. 同角的余角相等
C. 全等三角形的对应角相等
D. 线段垂直平分线上的点到线段两端的距离相等

答案： D

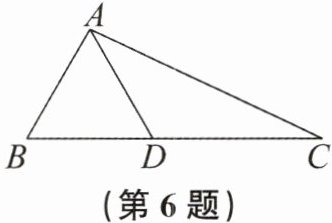
6. 如图,在 $ \triangle A B C $ 中,点 $ D $ 在 $ B C $ 上,且 $ B C = C D + A D $,则点 $ D $ 一定在线段AB的垂直平分线上。

答案： AB

7. 写出命题“如果两个实数相等,那么它们的绝对值相等”的逆命题：如果两个实数的绝对值相等，那么这两个实数相等。

答案： 如果两个实数的绝对值相等，那么这两个实数相等

8. 写出下列命题的逆命题,并判断逆命题是真命题还是假命题。若是假命题,请举反例说明。
(1)若 $ a ＞ b $,则 $ a ^ { 2 } ＞ b ^ { 2 } $。
(2)有一个角是 $ 60 ^ { \circ } $ 的三角形为等边三角形。
(3)等底等高的三角形面积相等。

答案：
(1) 逆命题：若 $ a ^ { 2 } ＞ b ^ { 2 } $，则 $ a ＞ b $。逆命题是假命题。反例：$ a = - 2 $，$ b = 1 $。（反例不唯一）
(2) 逆命题：等边三角形有一个角是 $ 60 ^ { \circ } $。逆命题是真命题。
(3) 逆命题：面积相等的三角形等底等高。逆命题是假命题。反例：底边长为 1、高为 8 的三角形与底边长为 4、高为 2 的三角形面积相等，但不是等底等高的。（反例不唯一）

9. 利用“线段垂直平分线定理及其逆定理”证明以下命题：
已知：如图,$ A B = A C $,$ D B = D C $,点 $ E $ 在 $ A D $ 上。求证：$ E B = E C $。
证明：由$AB = AC$，根据线段垂直平分线逆定理，点$A$在线段$BC$的垂直平分线上；由$DB = DC$，同理点$D$在线段$BC$的垂直平分线上，所以直线$AD$是线段$BC$的垂直平分线。又因为点$E$在$AD$上，根据线段垂直平分线定理，可得$EB = EC$。即证得$EB = EC$。

答案： 由$AB = AC$，根据线段垂直平分线逆定理，点$A$在线段$BC$的垂直平分线上；由$DB = DC$，同理点$D$在线段$BC$的垂直平分线上，所以直线$AD$是线段$BC$的垂直平分线。又因为点$E$在$AD$上，根据线段垂直平分线定理，可得$EB = EC$。即证得$EB = EC$。