2025年奔跑吧少年八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 在综合实践课上,同学们进行折纸活动,根据下列折纸的示意图(其中$C'$是点C的对应点),其中线段AD一定是$\triangle ABC$的中线的是 (
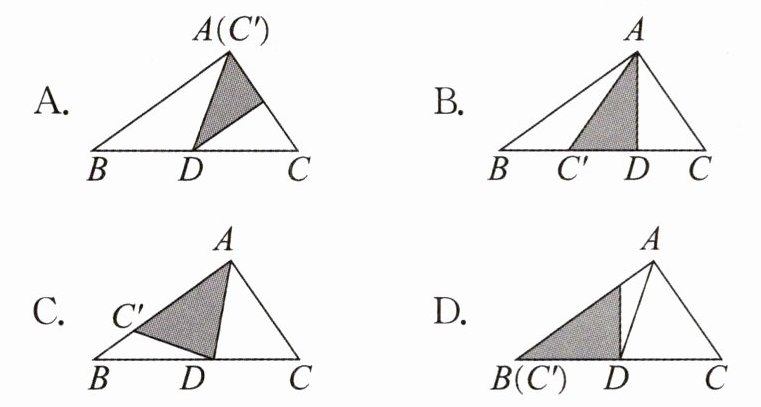
D
)
答案:
D
2. 判断命题“若$n>-3$,则$n^{2}>9$”是假命题,只需一个反例,反例中的n可以是 (
A. 4
B. -4
C. 3
D. -3
C
)A. 4
B. -4
C. 3
D. -3
答案:
C
3. 如图,在$\triangle ABC和\triangle ADE$中,$AB= AD$。添加下列条件,不能使$\triangle ABC\cong\triangle ADE$的是 (
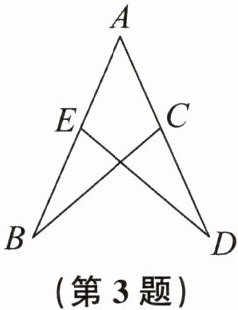
A. $\angle B= \angle D$
B. $\angle ACB= \angle AED$
C. $AC= AE$
D. $BC= DE$
D
)
A. $\angle B= \angle D$
B. $\angle ACB= \angle AED$
C. $AC= AE$
D. $BC= DE$
答案:
D
4. 如图,在$\triangle ABC$中,根据尺规作图痕迹,下列说法不一定正确的是 (
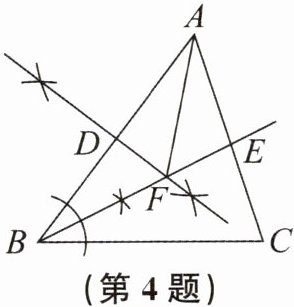
A. $AF= BF$
B. $DF\perp AB$
C. $\angle BAF= \angle CAF$
D. $\angle BAF= \angle EBC$
C
)
A. $AF= BF$
B. $DF\perp AB$
C. $\angle BAF= \angle CAF$
D. $\angle BAF= \angle EBC$
答案:
C
5. 如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,$\angle A= 62^{\circ}$,$\angle ACD= 35^{\circ}$,$\angle ABE= 40^{\circ}$,则$\angle BEC$的度数为
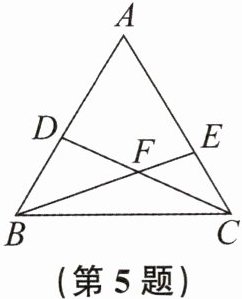
$102^{\circ}$
,$\angle BFC$的度数为$137^{\circ}$
。
答案:
$102^{\circ}$ $137^{\circ}$
6. 在$\triangle ABC$中,$\angle B= 35^{\circ}$,AD,AE分别是$\triangle ABC$的高线和角平分线,$\angle DCA= 75^{\circ}$,则$\angle DAE$的度数为
$20^{\circ}$或$35^{\circ}$
。
答案:
$20^{\circ}$或$35^{\circ}$
7. 如图,在$\triangle ABC$中($AB>BC$),$AC= 2BC$,BC边上的中线AD把$\triangle ABC$的周长分成60和40两部分,求AC和AB的长。
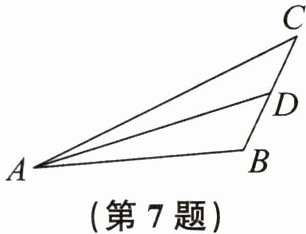
AC=

AC=
48
,AB=28
。
答案:
$AC = 48$,$AB = 28$。
8. 如图,在$\triangle ABC$中,$AB>AC$,AD为$\angle BAC$的平分线,P为线段AD上任意一点,连结PB,PC。求证:$AB-AC>PB-PC$。
证明:在$AB$上截取$AE = AC$,连接$PE$。
$\because AD$平分$\angle BAC$,$\therefore\angle 1=\angle 2$。
在$\triangle AEP$和$\triangle ACP$中,$\begin{cases}AE = AC\\\angle 1=\angle 2\\AP = AP\end{cases}$,$\therefore\triangle AEP\cong\triangle ACP(SAS)$,$\therefore PE = PC$。
在$\triangle PBE$中,$BE>PB - PE$(三角形三边关系)。
又$\because BE = AB - AE$,$AE = AC$,$PE = PC$,$\therefore AB - AC>PB - PC$。
故$AB - AC>PB - PC$得证。
证明:在$AB$上截取$AE = AC$,连接$PE$。
$\because AD$平分$\angle BAC$,$\therefore\angle 1=\angle 2$。
在$\triangle AEP$和$\triangle ACP$中,$\begin{cases}AE = AC\\\angle 1=\angle 2\\AP = AP\end{cases}$,$\therefore\triangle AEP\cong\triangle ACP(SAS)$,$\therefore PE = PC$。
在$\triangle PBE$中,$BE>PB - PE$(三角形三边关系)。
又$\because BE = AB - AE$,$AE = AC$,$PE = PC$,$\therefore AB - AC>PB - PC$。
故$AB - AC>PB - PC$得证。
答案:
在$AB$上截取$AE = AC$,连接$PE$。
$\because AD$平分$\angle BAC$,$\therefore\angle 1=\angle 2$。
在$\triangle AEP$和$\triangle ACP$中,$\begin{cases}AE = AC\\\angle 1=\angle 2\\AP = AP\end{cases}$,$\therefore\triangle AEP\cong\triangle ACP(SAS)$,$\therefore PE = PC$。
在$\triangle PBE$中,$BE>PB - PE$(三角形三边关系)。
又$\because BE = AB - AE$,$AE = AC$,$PE = PC$,$\therefore AB - AC>PB - PC$。
故$AB - AC>PB - PC$得证。
$\because AD$平分$\angle BAC$,$\therefore\angle 1=\angle 2$。
在$\triangle AEP$和$\triangle ACP$中,$\begin{cases}AE = AC\\\angle 1=\angle 2\\AP = AP\end{cases}$,$\therefore\triangle AEP\cong\triangle ACP(SAS)$,$\therefore PE = PC$。
在$\triangle PBE$中,$BE>PB - PE$(三角形三边关系)。
又$\because BE = AB - AE$,$AE = AC$,$PE = PC$,$\therefore AB - AC>PB - PC$。
故$AB - AC>PB - PC$得证。
查看更多完整答案,请扫码查看


