2025年奔跑吧少年八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
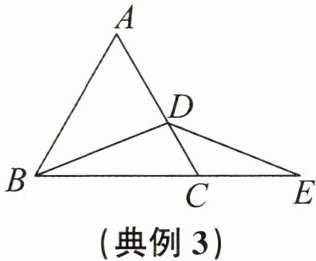
典例3 (2024秋·宁波海曙期末)如图,在等边三角形ABC中,D是AC边上的一点,E是BC延长线上的一点,且AD= CE。
(1)当D是AC的中点时,∠E的度数为______
(2)当D是AC边上的任意一点时,求证:DB= DE。
(1)当D是AC的中点时,∠E的度数为______
30°
。(2)当D是AC边上的任意一点时,求证:DB= DE。

答案:
(1)$30^{\circ}$
(2)略
(1)$30^{\circ}$
(2)略
互动题3-1 如图,△ABC是等边三角形,AD为BC边上的中线,AD= AE,则∠ADE的度数为______
75°
。
答案:
$75^{\circ}$
互动题3-2 (2024秋·温州期末)如图,在△ABC中,AB= AC,点D,E分别在BA,CB的延长线上,且AE= CD,∠BAE= ∠ACD。求证:△ABC是等边三角形。
证明:在△ABE和△CAD中,$\begin{cases}AB = AC\\\angle BAE=\angle ACD\\AE = CD\end{cases}$,所以△ABE≌△CAD
所以∠ABE=∠CAD。
因为AB = AC,所以∠ABC=∠ACB。
又因为∠ABE=∠ACB+∠BAC,∠CAD=∠BAC+∠BAD,所以∠ACB=∠BAD。
因为∠BAD + ∠BAC+∠CAD = 180°,∠ACB+∠BAC+∠ABC = 180°,且∠ABC=∠ACB,所以∠ABC=∠ACB=∠BAC。
所以△ABC是等边三角形
证明:在△ABE和△CAD中,$\begin{cases}AB = AC\\\angle BAE=\angle ACD\\AE = CD\end{cases}$,所以△ABE≌△CAD
SAS
。所以∠ABE=∠CAD。
因为AB = AC,所以∠ABC=∠ACB。
又因为∠ABE=∠ACB+∠BAC,∠CAD=∠BAC+∠BAD,所以∠ACB=∠BAD。
因为∠BAD + ∠BAC+∠CAD = 180°,∠ACB+∠BAC+∠ABC = 180°,且∠ABC=∠ACB,所以∠ABC=∠ACB=∠BAC。
所以△ABC是等边三角形
三个角都相等的三角形是等边三角形
。
答案:
在$\triangle ABE$和$\triangle CAD$中,$\begin{cases}AB = AC\\\angle BAE=\angle ACD\\AE = CD\end{cases}$,所以$\triangle ABE\cong\triangle CAD(SAS)$。
所以$\angle ABE=\angle CAD$。
因为$AB = AC$,所以$\angle ABC=\angle ACB$。
又因为$\angle ABE=\angle ACB+\angle BAC$,$\angle CAD=\angle BAC+\angle BAD$,所以$\angle ACB=\angle BAD$。
因为$\angle BAD + \angle BAC+\angle CAD = 180^{\circ}$,$\angle ACB+\angle BAC+\angle ABC = 180^{\circ}$,且$\angle ABC=\angle ACB$,所以$\angle ABC=\angle ACB=\angle BAC$。
所以$\triangle ABC$是等边三角形(三个角都相等的三角形是等边三角形)。
所以$\angle ABE=\angle CAD$。
因为$AB = AC$,所以$\angle ABC=\angle ACB$。
又因为$\angle ABE=\angle ACB+\angle BAC$,$\angle CAD=\angle BAC+\angle BAD$,所以$\angle ACB=\angle BAD$。
因为$\angle BAD + \angle BAC+\angle CAD = 180^{\circ}$,$\angle ACB+\angle BAC+\angle ABC = 180^{\circ}$,且$\angle ABC=\angle ACB$,所以$\angle ABC=\angle ACB=\angle BAC$。
所以$\triangle ABC$是等边三角形(三个角都相等的三角形是等边三角形)。
典例4 定理“等腰三角形的两个底角相等”的逆定理是 (
A. 有两个角相等的三角形是等腰三角形
B. 有两个底角相等的三角形是等腰三角形
C. 有两个角不相等的三角形不是等腰三角形
D. 不是等腰三角形的两个角不相等
A
)A. 有两个角相等的三角形是等腰三角形
B. 有两个底角相等的三角形是等腰三角形
C. 有两个角不相等的三角形不是等腰三角形
D. 不是等腰三角形的两个角不相等
答案:
A
互动题4 如图,AC= AD,BC= BD,则有 (
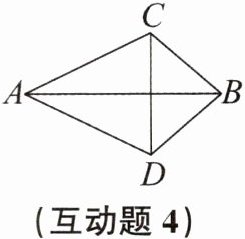
A. AB垂直平分CD
B. CD垂直平分AB
C. AB与CD互相垂直平分
D. CD平分∠ACB
A
)
A. AB垂直平分CD
B. CD垂直平分AB
C. AB与CD互相垂直平分
D. CD平分∠ACB
答案:
A
典例5 (2024秋·绍兴诸暨期末)如图,Rt△ABD和Rt△BCD分别位于BD异侧,∠DAB= ∠BCD= 90°,O是BD的中点,连结AC,AO,OC。
(1)若∠ADB= 30°,∠BDC= 40°,求∠AOC的度数。
(2)若锐角∠ADC= α,求∠AOC的度数(用含α的代数式表示)。

(1)若∠ADB= 30°,∠BDC= 40°,求∠AOC的度数。
140°
(2)若锐角∠ADC= α,求∠AOC的度数(用含α的代数式表示)。
2α

答案:
(1)$140^{\circ}$。
(2)$2\alpha$。
(1)$140^{\circ}$。
(2)$2\alpha$。
互动题5-1 如图,在Rt△ABC中,∠B= 90°,ED是线段AC的垂直平分线,交AC于点D,交BC于点E。已知∠BAE= 10°,则∠C的度数为______
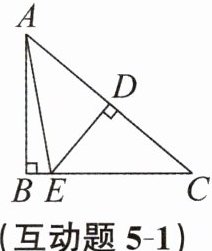
40°
。
答案:
$40^{\circ}$
(1)求证:△ADC≌△BDE。
证明:在△ADC和△BDE中,
(2)若BF= AH,求证:△FDH是等腰直角三角形。
证明:由(1)得△ADC≌△BDE,所以
在△BDF和△ADH中,
则
因为
又因为
证明:在△ADC和△BDE中,
$\begin{cases}AD = DB\\\angle ADC=\angle BDE\\DC = ED\end{cases}$
,所以△ADC≌△BDE(SAS)
。(2)若BF= AH,求证:△FDH是等腰直角三角形。
证明:由(1)得△ADC≌△BDE,所以
$\angle FBD=\angle HAD$
。在△BDF和△ADH中,
$\begin{cases}BF = AH\\\angle FBD=\angle HAD\\BD = AD\end{cases}$
,所以△BDF≌△ADH(SAS)
。则
$DF = DH$
,$\angle BDF=\angle ADH$
。因为
$\angle BDE=\angle BDF+\angle FDE = 90^{\circ}$
,所以$\angle ADH+\angle FDE = 90^{\circ}$
,即$\angle FDH = 90^{\circ}$
。又因为
$DF = DH$
,所以△FDH是等腰直角三角形。
答案:
$(1)$ 在$\triangle ADC$和$\triangle BDE$中,$\begin{cases}AD = DB\\\angle ADC=\angle BDE\\DC = ED\end{cases}$,所以$\triangle ADC\cong\triangle BDE(SAS)$。
$(2)$ 由$(1)$得$\triangle ADC\cong\triangle BDE$,所以$\angle FBD=\angle HAD$。
在$\triangle BDF$和$\triangle ADH$中,$\begin{cases}BF = AH\\\angle FBD=\angle HAD\\BD = AD\end{cases}$,所以$\triangle BDF\cong\triangle ADH(SAS)$。
则$DF = DH$,$\angle BDF=\angle ADH$。
因为$\angle BDE=\angle BDF+\angle FDE = 90^{\circ}$,所以$\angle ADH+\angle FDE = 90^{\circ}$,即$\angle FDH = 90^{\circ}$。
又因为$DF = DH$,所以$\triangle FDH$是等腰直角三角形。
$(2)$ 由$(1)$得$\triangle ADC\cong\triangle BDE$,所以$\angle FBD=\angle HAD$。
在$\triangle BDF$和$\triangle ADH$中,$\begin{cases}BF = AH\\\angle FBD=\angle HAD\\BD = AD\end{cases}$,所以$\triangle BDF\cong\triangle ADH(SAS)$。
则$DF = DH$,$\angle BDF=\angle ADH$。
因为$\angle BDE=\angle BDF+\angle FDE = 90^{\circ}$,所以$\angle ADH+\angle FDE = 90^{\circ}$,即$\angle FDH = 90^{\circ}$。
又因为$DF = DH$,所以$\triangle FDH$是等腰直角三角形。
查看更多完整答案,请扫码查看


