2025年奔跑吧少年八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
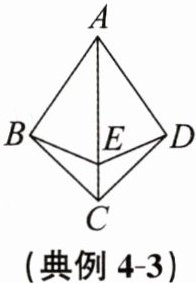
典例4-3 如图,$AB= AD$,$BC= DC$,点E在AC上。求证:
(1)AC平分$\angle BAD$。
证明:在$\triangle ABC$和$\triangle ADC$中,$\begin{cases}AB = AD \\ BC = DC \\ AC = AC\end{cases}$,
(2)$BE= DE$。
证明:在$\triangle ABE$和$\triangle ADE$中,$\begin{cases}AB = AD \\ \angle BAE=\angle DAE \\ AE = AE\end{cases}$,
(1)AC平分$\angle BAD$。
证明:在$\triangle ABC$和$\triangle ADC$中,$\begin{cases}AB = AD \\ BC = DC \\ AC = AC\end{cases}$,
$\triangle ABC\cong\triangle ADC(SSS)$
,$\therefore\angle BAC=\angle DAC$,即$AC$平分$\angle BAD$。(2)$BE= DE$。
证明:在$\triangle ABE$和$\triangle ADE$中,$\begin{cases}AB = AD \\ \angle BAE=\angle DAE \\ AE = AE\end{cases}$,
$\triangle ABE\cong\triangle ADE(SAS)$
,$\therefore BE = DE$。
答案:
(1) 在$\triangle ABC$和$\triangle ADC$中,$\begin{cases}AB = AD \\ BC = DC \\ AC = AC\end{cases}$,$\triangle ABC\cong\triangle ADC(SSS)$,$\therefore\angle BAC=\angle DAC$,即$AC$平分$\angle BAD$。
(2) 在$\triangle ABE$和$\triangle ADE$中,$\begin{cases}AB = AD \\ \angle BAE=\angle DAE \\ AE = AE\end{cases}$,$\triangle ABE\cong\triangle ADE(SAS)$,$\therefore BE = DE$。
(1) 在$\triangle ABC$和$\triangle ADC$中,$\begin{cases}AB = AD \\ BC = DC \\ AC = AC\end{cases}$,$\triangle ABC\cong\triangle ADC(SSS)$,$\therefore\angle BAC=\angle DAC$,即$AC$平分$\angle BAD$。
(2) 在$\triangle ABE$和$\triangle ADE$中,$\begin{cases}AB = AD \\ \angle BAE=\angle DAE \\ AE = AE\end{cases}$,$\triangle ABE\cong\triangle ADE(SAS)$,$\therefore BE = DE$。
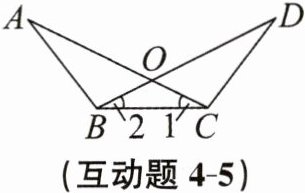
互动题4-5 如图,线段AC与线段BD相交于点O,连结AB,BC,CD,$\angle A= \angle D$,$OA= OD$。求证:$\angle 1= \angle 2$。
证明:在$\triangle AOB$和$\triangle DOC$中,
$\begin{cases}\angle A=\angle D\\OA = OD\\\angle AOB=\angle DOC\end{cases}$
$\therefore\triangle AOB\cong\triangle DOC(ASA)$
$\therefore OB = OC$(全等三角形对应边相等)
$\therefore\angle 1=\angle 2$(等腰三角形两底角相等)

证明:在$\triangle AOB$和$\triangle DOC$中,
$\begin{cases}\angle A=\angle D\\OA = OD\\\angle AOB=\angle DOC\end{cases}$
$\therefore\triangle AOB\cong\triangle DOC(ASA)$
$\therefore OB = OC$(全等三角形对应边相等)
$\therefore\angle 1=\angle 2$(等腰三角形两底角相等)
答案:
在$\triangle AOB$和$\triangle DOC$中,
$\begin{cases}\angle A=\angle D\\OA = OD\\\angle AOB=\angle DOC\end{cases}$
$\therefore\triangle AOB\cong\triangle DOC(ASA)$
$\therefore OB = OC$(全等三角形对应边相等)
$\therefore\angle 1=\angle 2$(等腰三角形两底角相等)
综上,$\boldsymbol{\angle 1=\angle 2}$得证。
$\begin{cases}\angle A=\angle D\\OA = OD\\\angle AOB=\angle DOC\end{cases}$
$\therefore\triangle AOB\cong\triangle DOC(ASA)$
$\therefore OB = OC$(全等三角形对应边相等)
$\therefore\angle 1=\angle 2$(等腰三角形两底角相等)
综上,$\boldsymbol{\angle 1=\angle 2}$得证。
典例5-1 (2024秋·杭州拱墅期末)如图,在$\triangle ABC$中,
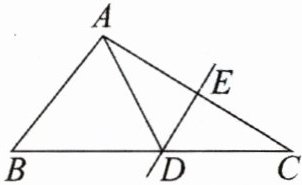
边AC的垂直平分线交AC于点E,交BC于点D。若$AB= 6$,$\triangle ABD$的周长为18,则BC的长为____

边AC的垂直平分线交AC于点E,交BC于点D。若$AB= 6$,$\triangle ABD$的周长为18,则BC的长为____
12
。
答案:
12
典例5-2 如图,$AB// CD$,BP和CP分别平分$\angle ABC和\angle DCB$,AD过点P,且与AB垂直。若$AD= 8$,求点P到BC的距离为
4
。
答案:
4。
互动题5-1 如图,在$\triangle ABC$中,$\angle C= 90^{\circ}$,BD平分$\angle ABC$,交AC于点D,过点D作$DE\perp AB$于点E,E恰好为AB的中点。若$DE= 1$,$DB= 2$,则AC的长为____
3
。
答案:
3
互动题5-2 如图,在$\triangle ABC$中,已知$AB= 10$,$AC= 8$,AD是$\angle BAC$的平分线,$DE\perp AC$于点E,且$DE= 4$。
(1)求$\triangle ABC$的面积。
(2)在解完(1)后,小智经过反思后发现$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}= \frac{AB}{AC}$,小慧发现$\frac{AB}{AC}= \frac{BD}{CD}$,小智和小慧的发现是否正确? 若正确,请写出证明过程;若错误,请说明理由。
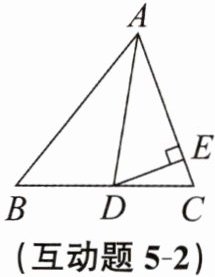
(1)求$\triangle ABC$的面积。
36
(2)在解完(1)后,小智经过反思后发现$\frac{S_{\triangle ABD}}{S_{\triangle ACD}}= \frac{AB}{AC}$,小慧发现$\frac{AB}{AC}= \frac{BD}{CD}$,小智和小慧的发现是否正确? 若正确,请写出证明过程;若错误,请说明理由。
小智和小慧的发现都正确,证明略。
答案:
(1)36。
(2)小智和小慧的发现都正确,证明略。
(1)36。
(2)小智和小慧的发现都正确,证明略。
查看更多完整答案,请扫码查看


