《2025年奔跑吧少年八年级数学上册浙教版》

9. 在$\triangle ABC$中,$AB^{2}= (a+b)^{2},AC^{2}= (a-b)^{2},BC^{2}= 4ab$,且$a＞b＞0$,则 (C)
A. $∠A= 90^{\circ }$
B. $∠B= 90^{\circ }$
C. $∠C= 90^{\circ }$
D. $∠C≠90^{\circ }$

答案： C

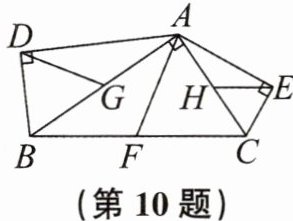
10. 如图,在$Rt\triangle ABC,Rt\triangle DBA,Rt\triangle EAC$中,DG,AF,EH均为斜边上的中线,则以DG,AF,EH为边构成的三角形是 (B)

A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 无法确定

答案： B

11. 在$\triangle ABC$中,$AB= 7,BC= 24,AC= 25,\triangle ABC$内存在一点P到三边的距离相等,这个距离为3。

答案： 3

12. 如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,“远航”号和“海天”号离开港口一个半小时后,分别位于点Q,R处,且相距30海里。若知道“远航”号沿北偏东$60^{\circ }$方向航行,请求出“海天”号的航行方向。
“海天”号沿北偏西 30°方向航行。

答案： “海天”号沿北偏西 30°方向航行。

13. 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作$∠PBQ= 60^{\circ }$,且$BP= BQ$,连结CQ。
(1)观察并猜想AP与CQ之间的数量关系,并说明理由。AP与CQ之间的数量关系是AP=CQ。
(2)若$PA= PC= 1,BP= \sqrt {2}$,求证:$PC⊥CQ$。证明见略。

答案：
(1)AP = CQ，理由略。
(2)略