《2025年奔跑吧少年八年级数学上册浙教版》

例1 如图,在△ABC中,AB= AC,点D在AB上,点F在AC的延长线上,且BD= CF,连结DF交BC于点E。求证：DE= EF。

证明：过点D作DG// AC交BC于点G。
∵ AB = AC，∴∠ B=∠ ACB。
∵ DG// AC，∴∠ DGB=∠ ACB，∠ DGE=∠ FCE，∴∠ B=∠ DGB，∴ BD = DG。
∵ BD = CF，∴ DG = CF。
在△ DGE和△ FCE中，$\begin{cases}\angle DGE=\angle FCE\\\angle DEG=\angle FEC\\DG = CF\end{cases}$，∴△ DGE≌△ FCE(AAS)。
∴ DE = EF。
故DE = EF得证。

答案： 过点$D$作$DG// AC$交$BC$于点$G$。
$\because AB = AC$，$\therefore\angle B=\angle ACB$。
$\because DG// AC$，$\therefore\angle DGB=\angle ACB$，$\angle DGE=\angle FCE$，$\therefore\angle B=\angle DGB$，$\therefore BD = DG$。
$\because BD = CF$，$\therefore DG = CF$。
在$\triangle DGE$和$\triangle FCE$中，$\begin{cases}\angle DGE=\angle FCE\\\angle DEG=\angle FEC\\DG = CF\end{cases}$，$\therefore\triangle DGE\cong\triangle FCE(AAS)$。
$\therefore DE = EF$。
故$DE = EF$得证。

跟踪训练1 如图,在等边三角形ABC中,点D在边AC的延长线上,延长BC至点E,使CE= AD,DG⊥BE于点G。求证：BG= EG。

证明：过点$D$作$DF// AB$交$BE$的延长线于$F$。
$\because\triangle ABC$是等边三角形，$\therefore\angle B=\angle ACB = 60^{\circ}$。
$\because DF// AB$，$\therefore\angle F=\angle B = 60^{\circ}$。
$\because\angle ACB=\angle DCF$，$\therefore\angle DCF = 60^{\circ}$，$\therefore\triangle DCF$是等边三角形，$\therefore DC = DF$。
$\because CE = AD$，$AD=AC + CD$，$EF=CE + CF$，$AC = BC$，$CD = CF$，$\therefore BC=EF$。
在$\triangle BDG$和$\triangle FDG$中，$\left\{\begin{array}{l}\angle BGD=\angle FGD\\\angle B=\angle F\\DG = DG\end{array}\right.$，$\therefore\triangle BDG\cong\triangle FDG(AAS)$，$\therefore BG = EG$。
综上，$\boldsymbol{BG = EG}$得证。

答案： 过点$D$作$DF// AB$交$BE$的延长线于$F$。
$\because\triangle ABC$是等边三角形，$\therefore\angle B=\angle ACB = 60^{\circ}$。
$\because DF// AB$，$\therefore\angle F=\angle B = 60^{\circ}$。
$\because\angle ACB=\angle DCF$，$\therefore\angle DCF = 60^{\circ}$，$\therefore\triangle DCF$是等边三角形，$\therefore DC = DF$。
$\because CE = AD$，$AD=AC + CD$，$EF=CE + CF$，$AC = BC$，$CD = CF$，$\therefore BC=EF$。
在$\triangle BDG$和$\triangle FDG$中，$\left\{\begin{array}{l}\angle BGD=\angle FGD\\\angle B=\angle F\\DG = DG\end{array}\right.$，$\therefore\triangle BDG\cong\triangle FDG(AAS)$，$\therefore BG = EG$。
综上，$\boldsymbol{BG = EG}$得证。

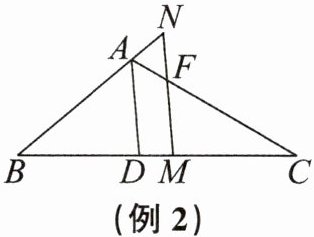
例2 如图,AD是△ABC的角平分线,M是BC边上一点(不与点B,D,C重合),过点M作MN//AD,交AC于点F,交BA的延长线于点N。
(1)求证：△AFN是等腰三角形。
(2)若∠B= 40°,∠C= 30°,求∠N的度数。55°

答案：
(1)略
(2)$55^{\circ }$。

跟踪训练2-1 如图,I是△ABC的角平分线BI,CI的交点,IE//AB,IF//AC,BC= 4,AB= 3,AC= 2,则△IEF的周长为 (D)
A. 2
B. 3
C. 4.5
D. 4

答案： D

跟踪训练2-2 如图,D是△ABC的边BC的延长线上一点,∠ABC和∠ACD的平分线相交于点O,过点O作OE//CB,分别交AB,AC于点E,F。若BE= 5,CF= 3,则EF的长为______2。

答案： 2

例3 如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,∠ABE= 2∠C。求证：AC-AB= 2BE。
证明：延长BE交AC于点F。
∵AE平分∠BAC，∴∠BAE = ∠FAE。
∵BE⊥AE，∴∠AEB=∠AEF = 90°。
在△ABE和△AFE中，$\left\{\begin{array}{l}\angle BAE=\angle FAE\\AE = AE\\\angle AEB=\angle AEF\end{array}\right.$，∴△ABE≌△AFE(ASA)。
∴AB = AF，BE = FE，∠ABE=∠AFE，∴BF = 2BE。
∵∠AFE=∠C+∠FBC，∠ABE = 2∠C，∴2∠C=∠C+∠FBC，∴∠FBC=∠C。
∴BF = FC。
∵FC=AC - AF，AF = AB，BF = 2BE，∴AC - AB=2BE。
故AC - AB = 2BE得证。

答案： 延长$BE$交$AC$于点$F$。
$\because AE$平分$\angle BAC$，$\therefore\angle BAE = \angle FAE$。
$\because BE\perp AE$，$\therefore\angle AEB=\angle AEF = 90^{\circ}$。
在$\triangle ABE$和$\triangle AFE$中，$\left\{\begin{array}{l}\angle BAE=\angle FAE\\AE = AE\\\angle AEB=\angle AEF\end{array}\right.$，$\therefore\triangle ABE\cong\triangle AFE(ASA)$。
$\therefore AB = AF$，$BE = FE$，$\angle ABE=\angle AFE$，$\therefore BF = 2BE$。
$\because\angle AFE=\angle C+\angle FBC$，$\angle ABE = 2\angle C$，$\therefore2\angle C=\angle C+\angle FBC$，$\therefore\angle FBC=\angle C$。
$\therefore BF = FC$。
$\because FC=AC - AF$，$AF = AB$，$BF = 2BE$，$\therefore AC - AB=2BE$。
故$AC - AB = 2BE$得证。

跟踪训练3 如图,在△ABC中,∠A= 90°,AB= AC,∠1= ∠2,CE⊥BD交BD的延长线于点E,试说明BD与CE之间的数量关系为BD=2CE。

答案： $BD = 2CE$。