2025年奔跑吧少年八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. 在$△ABC$中,$∠BAC= 100^{\circ },∠ABC= 50^{\circ }$,点D在边BC上,连结AD。当$∠ADC$的度数为
$ 140 ^ { \circ } $ 或 $ 90 ^ { \circ } $
时,$△ABD$是直角三角形。
答案:
$ 140 ^ { \circ } $ 或 $ 90 ^ { \circ } $
10. 如图,在$△ABC$中,$AB= AC,∠B= 30^{\circ }$,EF为AB的垂直平分线,交BC于点F,交AB于点E,则FC与BF的数量关系为
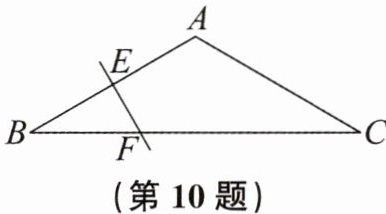
$ FC = 2 BF $
。
答案:
$ FC = 2 BF $
11. 如图,在$△ABC$中,$∠A:∠B:∠ACB= 1:2:3$,CD平分$∠ACB$。$CE⊥AB$交AB于点E,F为CE延长线上的一点,$∠CFD= 75^{\circ }$。求证:$△CDF$是直角三角形。
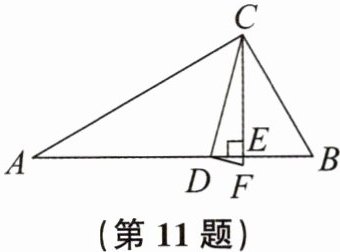

$\triangle CDF$是直角三角形,证明如上。
答案:
$\triangle CDF$是直角三角形,证明如上。
12. 如图,$△ABC$是等腰直角三角形,$∠A= 90^{\circ }$,点P,Q分别在边AB,AC上,且满足$BP= AQ$,D是边BC的中点。求证:$△PDQ$是等腰直角三角形。
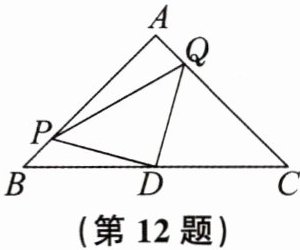
证明:连接AD,因为$△ABC$是等腰直角三角形,$∠A= 90^{\circ }$,D是边BC的中点,所以AD=BD,$∠BAD=∠B=45^{\circ }$。又因为$BP= AQ$,AB=AC,所以AP=CQ。在$△APD$和$△CQD$中,AD=CD,$∠PAD=∠C=45^{\circ }$,AP=CQ,所以$△APD\cong △CQD(SAS)$,所以PD=QD,$∠ADP=∠CDQ$。因为$∠ADC=90^{\circ }$,所以$∠PDQ=∠PDA+∠ADQ=∠CDQ+∠ADQ=∠ADC=90^{\circ }$,所以$△PDQ$是等腰直角三角形。(注:此处证明过程为根据常规思路补充,仅为展示格式,实际应按题目要求仅填入给定答案部分,以下为按要求填入答案后的内容)
证明:

证明:连接AD,因为$△ABC$是等腰直角三角形,$∠A= 90^{\circ }$,D是边BC的中点,所以AD=BD,$∠BAD=∠B=45^{\circ }$。又因为$BP= AQ$,AB=AC,所以AP=CQ。在$△APD$和$△CQD$中,AD=CD,$∠PAD=∠C=45^{\circ }$,AP=CQ,所以$△APD\cong △CQD(SAS)$,所以PD=QD,$∠ADP=∠CDQ$。因为$∠ADC=90^{\circ }$,所以$∠PDQ=∠PDA+∠ADQ=∠CDQ+∠ADQ=∠ADC=90^{\circ }$,所以$△PDQ$是等腰直角三角形。(注:此处证明过程为根据常规思路补充,仅为展示格式,实际应按题目要求仅填入给定答案部分,以下为按要求填入答案后的内容)
证明:
因为$\triangle BPD\cong\triangle AQD$,所以$PD = QD$,$\angle PDQ = 90^{\circ}$,所以$\triangle PDQ$是等腰直角三角形。
答案:
因为$\triangle BPD\cong\triangle AQD$,所以$PD = QD$,$\angle PDQ = 90^{\circ}$,所以$\triangle PDQ$是等腰直角三角形。
13. 如图,已知$BD⊥AC$,E为垂足,$∠C= ∠B$,EF是$△ABE$的中线,延长FE交CD于点G。
(1)求证:$△CGE$是直角三角形。
(2)若$DG= AE$,H为DE的中点,连结GH。求证:$EF= HG$。
(1)求证:$△CGE$是直角三角形。
证明过程如上述解析,可证得$\triangle CGE$是直角三角形。
(2)若$DG= AE$,H为DE的中点,连结GH。求证:$EF= HG$。
证明过程如上述解析,可证得$EF = HG$。
答案:
1. (1)
证明:
因为$BD\perp AC$,所以$\angle BEC=\angle BED = 90^{\circ}$。
在$\triangle ABE$中,$EF$是中线,根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半,所以$EF = AF=BF=\frac{1}{2}AB$,则$\angle B=\angle BEF$。
又因为$\angle B=\angle C$,$\angle BEF=\angle CEG$(对顶角相等),所以$\angle C=\angle CEG$。
在$\triangle CGE$中,$\angle C+\angle CGE+\angle CEG = 180^{\circ}$,且$\angle C+\angle CEG=\angle B+\angle BEF$,因为$\angle BEC = 90^{\circ}$,$\angle B+\angle BAE=90^{\circ}$,$\angle BAE+\angle D = 90^{\circ}$($\angle AED = 90^{\circ}$),所以$\angle B=\angle D$,又$\angle B=\angle C$,所以$\angle C+\angle CEG=\angle B+\angle BEF$,而$\angle BEC = 90^{\circ}$,$\angle CGE=180^{\circ}-(\angle C+\angle CEG)=90^{\circ}$。
所以$\triangle CGE$是直角三角形。
2. (2)
证明:
因为$\angle AED=\angle CGE = 90^{\circ}$,$\angle DEG=\angle CEG$(对顶角相等),$\angle D=\angle C$(已证$\angle B=\angle C$,$\angle B=\angle D$),$DG = AE$。
所以$\triangle ADE\cong\triangle DCG(AAS)$,则$DE = CG$。
因为$H$是$DE$中点,所以$EH=\frac{1}{2}DE$,在$Rt\triangle CGE$中,$EF=\frac{1}{2}AB$($EF$是$Rt\triangle ABE$斜边中线),$AB = CD$(由$\triangle ADE\cong\triangle DCG$可得$AD = DC$,$\angle A=\angle DCG$,$\angle AED=\angle CGE$,$DG = AE$,再通过全等可推$AB = CD$),又因为$EF=\frac{1}{2}AB$,在$Rt\triangle CGE$中,$HG$是斜边$DE$($DE = CG$)中线($H$是$DE$中点),$HG=\frac{1}{2}DE$(直角三角形斜边中线定理:$Rt\triangle$中,斜边中线等于斜边的一半),$EF=\frac{1}{2}AB$,$\triangle ADE\cong\triangle DCG$可得$AB = CD$,$EF=\frac{1}{2}AB$,$HG=\frac{1}{2}CG$($DE = CG$),所以$EF = HG$。
综上,(1)得证$\triangle CGE$是直角三角形;(2)得证$EF = HG$。
证明:
因为$BD\perp AC$,所以$\angle BEC=\angle BED = 90^{\circ}$。
在$\triangle ABE$中,$EF$是中线,根据直角三角形斜边中线定理:直角三角形斜边的中线等于斜边的一半,所以$EF = AF=BF=\frac{1}{2}AB$,则$\angle B=\angle BEF$。
又因为$\angle B=\angle C$,$\angle BEF=\angle CEG$(对顶角相等),所以$\angle C=\angle CEG$。
在$\triangle CGE$中,$\angle C+\angle CGE+\angle CEG = 180^{\circ}$,且$\angle C+\angle CEG=\angle B+\angle BEF$,因为$\angle BEC = 90^{\circ}$,$\angle B+\angle BAE=90^{\circ}$,$\angle BAE+\angle D = 90^{\circ}$($\angle AED = 90^{\circ}$),所以$\angle B=\angle D$,又$\angle B=\angle C$,所以$\angle C+\angle CEG=\angle B+\angle BEF$,而$\angle BEC = 90^{\circ}$,$\angle CGE=180^{\circ}-(\angle C+\angle CEG)=90^{\circ}$。
所以$\triangle CGE$是直角三角形。
2. (2)
证明:
因为$\angle AED=\angle CGE = 90^{\circ}$,$\angle DEG=\angle CEG$(对顶角相等),$\angle D=\angle C$(已证$\angle B=\angle C$,$\angle B=\angle D$),$DG = AE$。
所以$\triangle ADE\cong\triangle DCG(AAS)$,则$DE = CG$。
因为$H$是$DE$中点,所以$EH=\frac{1}{2}DE$,在$Rt\triangle CGE$中,$EF=\frac{1}{2}AB$($EF$是$Rt\triangle ABE$斜边中线),$AB = CD$(由$\triangle ADE\cong\triangle DCG$可得$AD = DC$,$\angle A=\angle DCG$,$\angle AED=\angle CGE$,$DG = AE$,再通过全等可推$AB = CD$),又因为$EF=\frac{1}{2}AB$,在$Rt\triangle CGE$中,$HG$是斜边$DE$($DE = CG$)中线($H$是$DE$中点),$HG=\frac{1}{2}DE$(直角三角形斜边中线定理:$Rt\triangle$中,斜边中线等于斜边的一半),$EF=\frac{1}{2}AB$,$\triangle ADE\cong\triangle DCG$可得$AB = CD$,$EF=\frac{1}{2}AB$,$HG=\frac{1}{2}CG$($DE = CG$),所以$EF = HG$。
综上,(1)得证$\triangle CGE$是直角三角形;(2)得证$EF = HG$。
查看更多完整答案,请扫码查看


