《2025年奔跑吧少年八年级数学上册浙教版》

10. 已知下列命题：①等腰三角形底边上的高线与顶角平分线互相重合；②若 $ a = b $,则 $ \frac { a } { c } = \frac { b } { c } ( c \neq 0 ) $；③若三角形的三条边分别为 4,5,4,则这个三角形是等腰三角形；④若 $ C $ 是线段 $ A B $ 的中点,则 $ A C = C B $。其中原命题和逆命题都是真命题的有(D)
A. ①②④
B. ②③
C. ①③④
D. ①②

答案： D

11. 写出下列定理的逆命题,并判断原定理和逆命题是否互为逆定理。
(1)对顶角相等。
(2)在同一个三角形中,等边对等角。

答案：
(1) 逆命题：相等的角是对顶角。原定理和逆命题不互为逆定理。
(2) 逆命题：在同一个三角形中，等角对等边。原定理和逆命题互为逆定理。

12. 如图,在 $ \triangle A B C $ 中,$ \angle A C B = 90 ^ { \circ } $,$ D $ 是 $ B C $ 延长线上的一点,$ B D $ 的垂直平分线 $ E G $ 交 $ A B $ 于点 $ E $,连结 $ D E $ 交 $ A C $ 于点 $ F $。求证：点 $ E $ 在 $ A F $ 的垂直平分线上。
证明：因为$EG$是$BD$的垂直平分线，所以$EB = ED$，则$\angle B=\angle D$。由于$\angle ACB = 90^{\circ}$，所以$\angle A+\angle B=90^{\circ}$，$\angle D+\angle DFC = 90^{\circ}$。又$\angle AFE=\angle DFC$（对顶角相等），且$\angle B=\angle D$，故$\angle A=\angle AFE$，所以$EA = EF$。根据线段垂直平分线的判定，点$E$在$AF$的垂直平分线上。

答案： 因为$EG$是$BD$的垂直平分线，所以$EB = ED$，则$\angle B=\angle D$。
由于$\angle ACB = 90^{\circ}$，所以$\angle A+\angle B=90^{\circ}$，$\angle D+\angle DFC = 90^{\circ}$。
又$\angle AFE=\angle DFC$（对顶角相等），且$\angle B=\angle D$，故$\angle A=\angle AFE$，所以$EA = EF$。
根据线段垂直平分线的判定，点$E$在$AF$的垂直平分线上。

13. 写出定理“等腰三角形底边上的中线与顶角平分线互相重合”的逆命题,并判断此逆命题是真命题还是假命题,若是真命题,请给出证明(需画出图形,写出已知、求证,再证明)；若是假命题,请举反例说明。

答案： 逆命题：如果一个三角形一边上的中线与这条边所对的角的平分线互相重合，那么这个三角形是等腰三角形。此逆命题是真命题。证明略。

14. 如图,已知 $ \triangle A B C $ 是等边三角形。
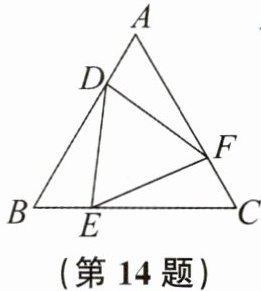
(1)若 $ A D = B E = C F $,求证：$ \triangle D E F $ 是等边三角形。
证明：略
(2)请问(1)中的逆命题成立吗？若成立,请给出证明；若不成立,请举反例说明。
成立，证明略。

答案：
(1) 略
(2) 成立，证明略。