《2025年奔跑吧少年八年级数学上册浙教版》

1. 已知$∠A= 37^{\circ },∠B= 53^{\circ }$,则$△ABC$为(C)
A. 锐角三角形
B. 钝角三角形
C. 直角三角形
D. 以上都有可能

答案： C

2. 根据下列条件不能判断$△ABC$是直角三角形的为(C)
A. $∠B= ∠C= 45^{\circ }$
B. $∠A,∠B,∠C的度数比为3:1:2$
C. $∠A-∠B= 90^{\circ }$
D. $∠A-∠C= ∠B$

答案： C

3. 如图,在$△ABC$中,$∠B+∠C= 90^{\circ }$,AD是BC边上的高线,E是BC的中点,连结AE,则图中直角三角形的个数是(C)

A. 2
B. 3
C. 4
D. 5

答案： C

4. 在$△ABC$中,若$∠A= \frac {1}{2}∠B= ∠C$,则下面对$△ABC$的形状描述最准确的是(B)
A. 等腰三角形
B. 等腰直角三角形
C. 等边三角形
D. 直角三角形

答案： B

5. 把等边三角形ABC的一边AB延长一倍到点D,连结CD,则$△ADC$是(B)
A. 等腰三角形
B. 直角三角形
C. 等边三角形
D. 不能确定

答案： B

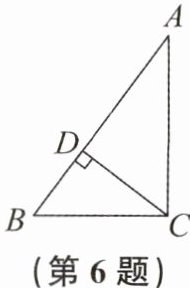
6. 如图,在$△ABC$中,CD是AB边上的高线。若$∠A= ∠DCB$,则$∠BCA$的度数为$ 90 ^ { \circ } $。

答案： $ 90 ^ { \circ } $

7. 如图,在$△ABC$中,AD是边BC上的高线,E是边AB上的一点,CE交AD于点M,且$∠DCM= ∠MAE$。求证：$△AEM$是直角三角形。

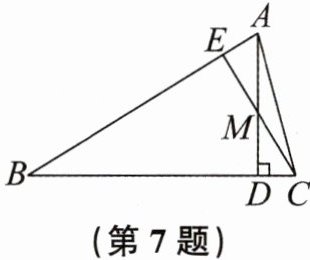
证明：因为$\angle AEM = 90^{\circ}$，所以$\triangle AEM$是直角三角形。

答案： 因为$\angle AEM = 90^{\circ}$，所以$\triangle AEM$是直角三角形。

8. 如图,已知$AB// CD$,$∠BEF与∠DFE$的平分线相交于点G,$△EFG$是直角三角形吗？请说明理由。

$ \triangle EFG $ 是直角三角形，理由略。

答案： $ \triangle EFG $ 是直角三角形，理由略。