《2025年奔跑吧少年八年级数学上册浙教版》

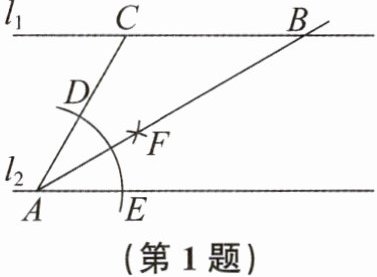
1. 如图,直线l₁//l₂,点C,A分别在l₁,l₂上,以点A为圆心,适当长为半径画弧,分别交AC,l₂于点D,E,分别以D,E为圆心,大于$\frac{1}{2}DE$长为半径画弧,两弧相交于点F,作射线AF交l₁于点B。若∠BCA= 120°,则∠BAE的度数为 (C)

A. 20°
B. 25°
C. 30°
D. 50°

答案： C

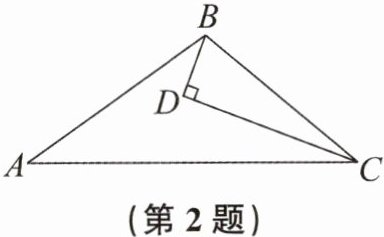
2. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD于点D,∠ABD= ∠A。若BD= 1,BC= 3,则AC的长为 (D)

A. 2
B. 3
C. 4
D. 5

答案： D

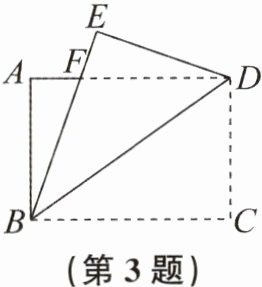
3. 如图,把一张长方形纸片沿对角线折叠,则图中一定是等腰三角形的是______$\triangle BFD$(不另外添加辅助线)。

答案： $\triangle BFD$

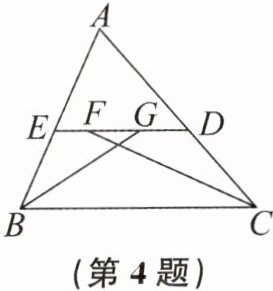
4. 如图,在△ABC中,ED//BC,∠ABC和∠ACB的平分线分别交ED于点G,F。若FG= 3,ED= 7,则EB+DC的值为______10。

答案： 10

5. 如图,在等边三角形ABC中,D为AC边上一动点,E为AB延长线上一动点,DE交CB于点P,P为DE的中点。求证：CD= BE。

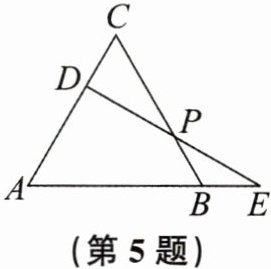
证明：过点$D$作$DF// AB$，交$BC$于点$F$。
$\because\triangle ABC$是等边三角形，$\therefore\angle A=\angle ABC=\angle C = 60^{\circ}$。
$\because DF// AB$，$\therefore\angle CDF=\angle A = 60^{\circ}$，$\angle DFC=\angle ABC = 60^{\circ}$。
$\therefore\triangle CDF$是等边三角形，$\therefore CD = DF$。
$\because P$为$DE$的中点，$\therefore DP = EP$。
$\because DF// AB$，$\therefore\angle PDF=\angle E$。
在$\triangle DPF$和$\triangle EPB$中，$\begin{cases}\angle PDF=\angle E\\DP = EP\\\angle DPF=\angle EPB\end{cases}$
$\therefore\triangle DPF\cong\triangle EPB(ASA)$，$\therefore DF = BE$。
又$\because CD = DF$，$\therefore CD = BE$。
综上，$CD = BE$得证。

答案： 过点$D$作$DF// AB$，交$BC$于点$F$。
$\because\triangle ABC$是等边三角形，$\therefore\angle A=\angle ABC=\angle C = 60^{\circ}$。
$\because DF// AB$，$\therefore\angle CDF=\angle A = 60^{\circ}$，$\angle DFC=\angle ABC = 60^{\circ}$。
$\therefore\triangle CDF$是等边三角形，$\therefore CD = DF$。
$\because P$为$DE$的中点，$\therefore DP = EP$。
$\because DF// AB$，$\therefore\angle PDF=\angle E$。
在$\triangle DPF$和$\triangle EPB$中，$\begin{cases}\angle PDF=\angle E\\DP = EP\\\angle DPF=\angle EPB\end{cases}$
$\therefore\triangle DPF\cong\triangle EPB(ASA)$，$\therefore DF = BE$。
又$\because CD = DF$，$\therefore CD = BE$。
综上，**$CD = BE$得证**。

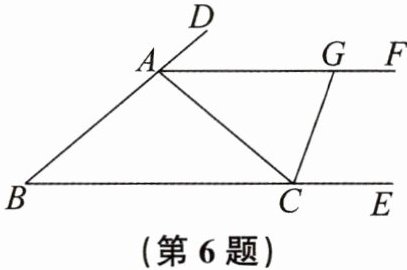
6. 如图,已知D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,且AF//BC。
(1)求证：△ABC是等腰三角形。
(2)如图,作∠ACE的平分线交AF于点G,若∠B= 40°,求∠AGC的度数。(70°)

答案：
(1)略
(2)$70^{\circ }$。