2025年奔跑吧少年八年级数学上册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年八年级数学上册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,在△ABC中,∠B= ∠C,D为边BC的中点,过点D分别向AB,AC作垂线段,则能够说明△BDE≌△CDF的理由是 (
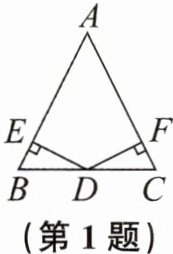
A. SSS
B. SAS
C. AAS
D. 无法确定
C
)
A. SSS
B. SAS
C. AAS
D. 无法确定
答案:
C
2. 如图,在△ACD和△BCE中,CA= CB,AD= BE,CD= CE,∠ACE= 60°,∠BCD= 150°,则∠BCA的度数为 (

A. 60°
B. 50°
C. 45°
D. 40°
C
)
A. 60°
B. 50°
C. 45°
D. 40°
答案:
C
3. 在如图所示的三角形纸片中,AB= 8cm,BC= 6cm,AC= 5cm,沿过点B的直线折叠这个三角形,使点C落在AB上的点E处,折痕为BD,则△AED的周长为 (

A. 7cm
B. 11cm
C. 13cm
D. 14cm
A
)
A. 7cm
B. 11cm
C. 13cm
D. 14cm
答案:
A
4. 如图,△ABC平移后得到△DEF,∠A= 55°,∠B= 45°,则∠DFE的度数为
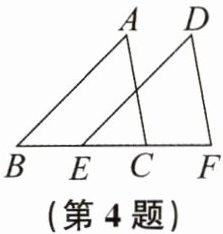
80°
。
答案:
$80^{\circ }$
5. 如图,AB= DE,CD= AC,∠BAC= ∠D,AF⊥CD于点F。若∠BCE= 63°,则∠CAF的度数为______

27°
。
答案:
$27^{\circ }$
6. 如图,已知A,B,D,E在同一直线上,AD= BE,BC//EF,∠A= ∠EDF。求证:△ABC≌△DEF。
证明:∵AD=BE,
∴AD-BD=BE-BD,即AB=DE。
∵BC//EF,
∴∠ABC=∠DEF。
在△ABC和△DEF中,
$\begin{cases}\angle A=\angle EDF\\AB = DE\\\angle ABC=\angle DEF\end{cases}$
所以△ABC≌△DEF(
证明:∵AD=BE,
∴AD-BD=BE-BD,即AB=DE。
∵BC//EF,
∴∠ABC=∠DEF。
在△ABC和△DEF中,
$\begin{cases}\angle A=\angle EDF\\AB = DE\\\angle ABC=\angle DEF\end{cases}$
所以△ABC≌△DEF(
ASA
)。
答案:
在$\triangle ABC$和$\triangle DEF$中,
$\begin{cases}\angle A=\angle EDF\\AB = DE\\\angle ABC=\angle DEF\end{cases}$
所以$\triangle ABC\cong\triangle DEF(ASA)$。
$\begin{cases}\angle A=\angle EDF\\AB = DE\\\angle ABC=\angle DEF\end{cases}$
所以$\triangle ABC\cong\triangle DEF(ASA)$。
7. 如图,已知AB= AE,AC= AD,∠BAD= ∠EAC。
(1)△ADE与△ACB是否全等?请说明理由。
(2)若∠B= 35°,∠D= 45°,求∠DAE的度数。

(1)△ADE与△ACB是否全等?请说明理由。
答:
(2)若∠B= 35°,∠D= 45°,求∠DAE的度数。
答:
(1)△ADE与△ACB是否全等?请说明理由。
(2)若∠B= 35°,∠D= 45°,求∠DAE的度数。

(1)△ADE与△ACB是否全等?请说明理由。
答:
△ADE与△ACB全等,理由略
(2)若∠B= 35°,∠D= 45°,求∠DAE的度数。
答:
100°
答案:
(1)$\triangle ADE$与$\triangle ACB$全等,理由略。
(2)$100^{\circ }$。
(1)$\triangle ADE$与$\triangle ACB$全等,理由略。
(2)$100^{\circ }$。
8. 如图,∠D+∠DAB= 180°,在四边形ABCD的边AB,CD上截取线段AF,CE,使AF= CE,连结EF,M,N是线段EF上的两点,且EM= FN,连结AN,CM。求证:AN//CM。
证明:∵∠D+∠DAB= 180°,∴
证明:∵∠D+∠DAB= 180°,∴
AB// CD
,∴∠AFN=∠CEM
。∵AF= CE,EM= FN,∴△AFN≌△CEM(SAS)
,∴∠ANF=∠CME
,∴∠ANM=∠CMN
,∴AN// CM。
答案:
由$\angle D+\angle DAB = 180^{\circ}$得$AB// CD$,进而$\angle AFN=\angle CEM$,结合$AF = CE$,$EM = FN$证得$\triangle AFN\cong\triangle CEM(SAS)$,得出$\angle ANF=\angle CME$,再推出$\angle ANM=\angle CMN$,所以$AN// CM$。
查看更多完整答案,请扫码查看


