2025年全练单元卷九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全练单元卷九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
27. (10分)如图,在平面直角坐标系$xOy$中,矩形$OABC$的边$OA$在$x$轴上,$OC$在$y$轴上,$OA = 4$,$OC = 2$,点$D$是$BC$边上的动点(不与$B$,$C$重合),反比例函数$y = \frac{k}{x}(k > 0,x > 0)$的图象经过点$D$,且与$AB$交于点$E$,连接$OD$,$OE$,$DE$.
(1)若点$D$的横坐标为1.
①求$k$的值;
②点$P$在$x$轴上,当$\triangle ODE$的面积等于$\triangle ODP$的面积时,试求点$P$的坐标;
(2)延长$ED$交$y$轴于点$F$,连接$AC$,判断四边形$AEFC$的形状,并说明理由.
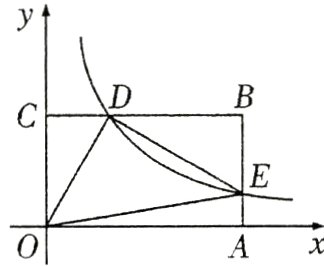
(1)若点$D$的横坐标为1.
①求$k$的值;
②点$P$在$x$轴上,当$\triangle ODE$的面积等于$\triangle ODP$的面积时,试求点$P$的坐标;
(2)延长$ED$交$y$轴于点$F$,连接$AC$,判断四边形$AEFC$的形状,并说明理由.

答案:
解:
(1)①
∵点$D$的横坐标为$1$,$OC = 2$,
∴点$D$的坐标为$(1,2)$,
∵反比例函数$y = \frac{k}{x}(k > 0,x > 0)$的图象经过点$D$,
∴$k = 1\times2 = 2$;
②
∵点$D$的横坐标为$1$,$OC = 2$,
∴$S_{\triangle COD} = 1$,
∵点$E$在反比例函数$y = \frac{2}{x}$的图象上,
∴$S_{\triangle AOE} = 1$,
∵$OA = 4$,
∴$AE = \frac{1}{2}$,$BD = 4 - 1 = 3$,$BE = 2 - \frac{1}{2} = \frac{3}{2}$,
∴$S_{\triangle ODE} = S_{矩形OABC} - S_{\triangle OCD} - S_{\triangle AOE} - S_{\triangle BDE} = 2\times4 - 1 - 1 - \frac{1}{2} \times 3 \times \frac{3}{2} = \frac{15}{4}$,
∵点$P$在$x$轴上,
∴设$P(m,0)$,
∴$S_{\triangle ODP} = \frac{1}{2}|m|\times2 = \frac{15}{4}$,解得$m = \pm\frac{15}{4}$,
∴点$P$的坐标为$(\frac{15}{4},0)$或$(-\frac{15}{4},0)$;
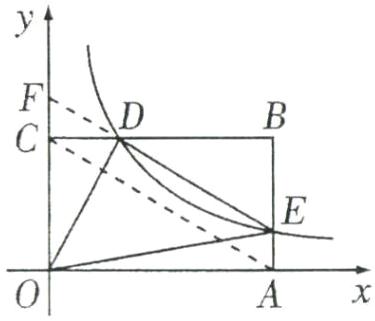
(2)四边形$AEFC$是平行四边形,
理由如下:如图,连接$AC$,延长$ED$交$y$轴于点$F$,
由题意得$D(\frac{k}{2},2)$,$E(4,\frac{k}{4})$,
设直线$EF$的函数解析式为$y = ax + b(a \neq 0)$,
则$\begin{cases}2 = \frac{k}{2}a + b \\ \frac{k}{4} = 4a + b \end{cases}$,解得$\begin{cases}a = -\frac{1}{2} \\ b = \frac{8 + k}{4} \end{cases}$,
∴直线$EF$的函数解析式为$y = -\frac{1}{2}x + \frac{8 + k}{4}$,
∴$OF = \frac{8 + k}{4}$,
∴$CF = OF - 2 = \frac{k}{4} = AE$,
又
∵$CF// AE$,
∴四边形$AEFC$是平行四边形.
解:
(1)①
∵点$D$的横坐标为$1$,$OC = 2$,
∴点$D$的坐标为$(1,2)$,
∵反比例函数$y = \frac{k}{x}(k > 0,x > 0)$的图象经过点$D$,
∴$k = 1\times2 = 2$;
②
∵点$D$的横坐标为$1$,$OC = 2$,
∴$S_{\triangle COD} = 1$,
∵点$E$在反比例函数$y = \frac{2}{x}$的图象上,
∴$S_{\triangle AOE} = 1$,
∵$OA = 4$,
∴$AE = \frac{1}{2}$,$BD = 4 - 1 = 3$,$BE = 2 - \frac{1}{2} = \frac{3}{2}$,
∴$S_{\triangle ODE} = S_{矩形OABC} - S_{\triangle OCD} - S_{\triangle AOE} - S_{\triangle BDE} = 2\times4 - 1 - 1 - \frac{1}{2} \times 3 \times \frac{3}{2} = \frac{15}{4}$,
∵点$P$在$x$轴上,
∴设$P(m,0)$,
∴$S_{\triangle ODP} = \frac{1}{2}|m|\times2 = \frac{15}{4}$,解得$m = \pm\frac{15}{4}$,
∴点$P$的坐标为$(\frac{15}{4},0)$或$(-\frac{15}{4},0)$;
(2)四边形$AEFC$是平行四边形,
理由如下:如图,连接$AC$,延长$ED$交$y$轴于点$F$,
由题意得$D(\frac{k}{2},2)$,$E(4,\frac{k}{4})$,
设直线$EF$的函数解析式为$y = ax + b(a \neq 0)$,
则$\begin{cases}2 = \frac{k}{2}a + b \\ \frac{k}{4} = 4a + b \end{cases}$,解得$\begin{cases}a = -\frac{1}{2} \\ b = \frac{8 + k}{4} \end{cases}$,
∴直线$EF$的函数解析式为$y = -\frac{1}{2}x + \frac{8 + k}{4}$,
∴$OF = \frac{8 + k}{4}$,
∴$CF = OF - 2 = \frac{k}{4} = AE$,
又
∵$CF// AE$,
∴四边形$AEFC$是平行四边形.

查看更多完整答案,请扫码查看


