2025年全练单元卷九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全练单元卷九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (8分)计算:
(1)$\sqrt{8}\times\sin45^{\circ}-2025^{0}+2^{-1}$;
(2)$(\pi-\sqrt{5})^{0}+\sqrt{4}+(-1)^{2025}-\sqrt{3}\tan60^{\circ}$.
(1)$\sqrt{8}\times\sin45^{\circ}-2025^{0}+2^{-1}$;
(2)$(\pi-\sqrt{5})^{0}+\sqrt{4}+(-1)^{2025}-\sqrt{3}\tan60^{\circ}$.
答案:
解:
(1)原式$=2\sqrt{2}×\frac{\sqrt{2}}{2}-1+\frac{1}{2}=1\frac{1}{2}$;
(2)原式$=1 + 2 - 1-\sqrt{3}×\sqrt{3}=2 - 3 = -1$.
(1)原式$=2\sqrt{2}×\frac{\sqrt{2}}{2}-1+\frac{1}{2}=1\frac{1}{2}$;
(2)原式$=1 + 2 - 1-\sqrt{3}×\sqrt{3}=2 - 3 = -1$.
22. (8分)如图,在$\triangle ABC$中,$AD$是$BC$上的高,$\tan B = \cos\angle DAC$.
(1)求证:$AC = BD$;
(2)若$\sin C = \frac{12}{13}$,$BC = 12$,求$AD$的长.
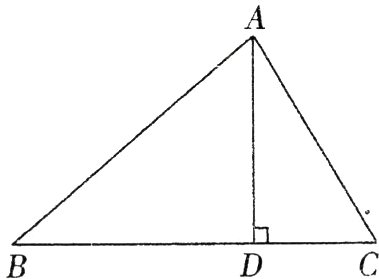
(1)求证:$AC = BD$;
(2)若$\sin C = \frac{12}{13}$,$BC = 12$,求$AD$的长.

答案:
(1)证明:$\because AD$是$BC$上的高,$\therefore AD\perp BC$,$\therefore \angle ADB = 90^{\circ},\angle ADC = 90^{\circ}$. 在$Rt\triangle ABD$和$Rt\triangle ADC$中,$\tan B=\frac{AD}{BD},\cos\angle DAC=\frac{AD}{AC}$,又$\because \tan B = \cos\angle DAC,\therefore \frac{AD}{BD}=\frac{AD}{AC}$,$\therefore AC = BD$;
(2)解:在$Rt\triangle ADC$中,$\sin C=\frac{12}{13}$,故可知$AD = 12k,AC = 13k$,$\therefore CD=\sqrt{AC^{2}-AD^{2}} = 5k$,$\because BC = BD + CD,AC = BD$,$\therefore BC = AC + CD = 13k + 5k = 18k$,$\because BC = 12,\therefore 18k = 12,\therefore k=\frac{2}{3}$,$\therefore AD = 12k = 12×\frac{2}{3}=8$.
(1)证明:$\because AD$是$BC$上的高,$\therefore AD\perp BC$,$\therefore \angle ADB = 90^{\circ},\angle ADC = 90^{\circ}$. 在$Rt\triangle ABD$和$Rt\triangle ADC$中,$\tan B=\frac{AD}{BD},\cos\angle DAC=\frac{AD}{AC}$,又$\because \tan B = \cos\angle DAC,\therefore \frac{AD}{BD}=\frac{AD}{AC}$,$\therefore AC = BD$;
(2)解:在$Rt\triangle ADC$中,$\sin C=\frac{12}{13}$,故可知$AD = 12k,AC = 13k$,$\therefore CD=\sqrt{AC^{2}-AD^{2}} = 5k$,$\because BC = BD + CD,AC = BD$,$\therefore BC = AC + CD = 13k + 5k = 18k$,$\because BC = 12,\therefore 18k = 12,\therefore k=\frac{2}{3}$,$\therefore AD = 12k = 12×\frac{2}{3}=8$.
查看更多完整答案,请扫码查看


