《2025年全练单元卷九年级数学下册人教版》

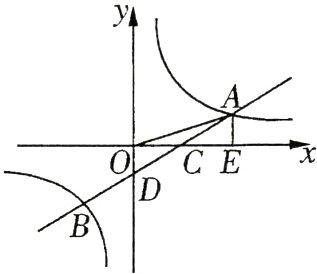
26. (10分)如图，一次函数$y = ax + b$的图象与反比例函数$y = \frac{k}{x}$的图象交于A，B两点，与x轴交于点C，与y轴交于点D，AE垂直x轴于E点，已知$OA = \sqrt{10}$，$OE = 3AE$，点B的坐标为$(m,-2)$.
(1)求反比例函数的解析式；
(2)求一次函数的解析式；
(3)在y轴上存在一点P，使得△PDC与△ODC相似，请求出P点的坐标.

答案：
解：
(1)
∵ $OE = 3AE$，$OA = \sqrt{10}$，
∴ 在$Rt\triangle AOE$中，根据勾股定理得$OE^2 + AE^2 = OA^2$，
即$OE^2 + AE^2 = 10$，
∴ $AE = 1$，$OE = 3$，
∴ 点$A$的坐标为(3,1).
∵ $A$点在双曲线上，
∴ $1 = \frac{k}{3}$，即$k = 3$，
则反比例函数的解析式为$y = \frac{3}{x}$；
(2)
∵ 点$B(m,-2)$在双曲线$y = \frac{3}{x}$上，
∴ $-2 = \frac{3}{m}$，
∴ $m = -\frac{3}{2}$，
∴ 点$B$的坐标为$(-\frac{3}{2},-2)$，
把$A$，$B$的坐标代入$y = ax + b$得
$\begin{cases}3a + b = 1\\-\frac{3}{2}a + b = -2\end{cases}$，解得$\begin{cases}a = \frac{2}{3}\\b = -1\end{cases}$，
则一次函数的解析式为$y = \frac{2}{3}x - 1$；
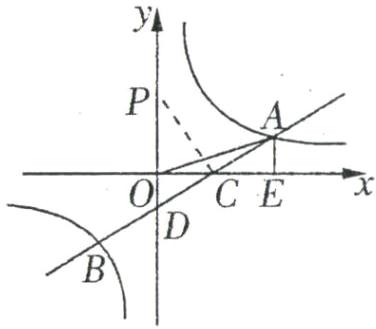
(3)过点$C$作$CP\perp AB$，交$y$轴于点$P$，
∵ $C$，$D$两点在直线$y = \frac{2}{3}x - 1$上，
∴ $C$，$D$的坐标分别是$C(\frac{3}{2},0)$，$D(0,-1)$，
即$OC = \frac{3}{2}$，$OD = 1$，
∴ $DC = \frac{\sqrt{13}}{2}$，
∵ $\triangle PDC\sim\triangle CDO$，
∴ $\frac{PD}{DC}=\frac{DC}{OD}$，
∴ $PD = \frac{DC^2}{OD}=\frac{13}{4}$，
又$OP = DP - OD = \frac{13}{4}-1 = \frac{9}{4}$，
∴ $P$点坐标为$(0,\frac{9}{4})$.