2025年全练单元卷九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全练单元卷九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
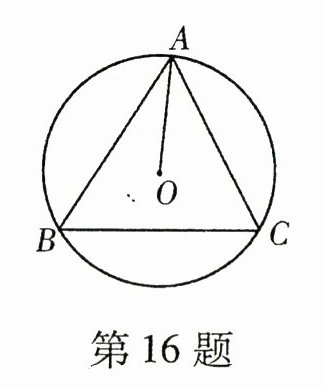
16. 如图所示,△ABC内接于⊙O,AO = 2,BC = $2\sqrt{3}$,则∠BAC的度数为_______.

答案:
60°
17. 在△ABC中,∠C = 90°,AB = 2BC,现给出下列结论:①$\sin A = \frac{\sqrt{3}}{2}$;②$\cos B = \frac{1}{2}$;③$\tan A = \frac{\sqrt{3}}{3}$;④$\tan B = \sqrt{3}$,其中正确的结论是_______.(只需填上正确结论的序号)
答案:
②③④
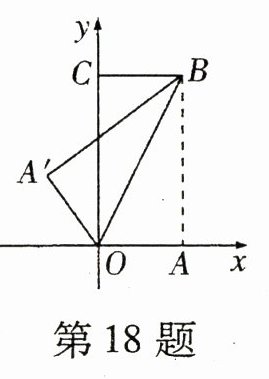
18. 如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A′的位置,若OB = 2,$\sin\angle BOC = \frac{1}{2}$,则点A′的坐标为__________.

答案:
(−$\frac{1}{2}$昼
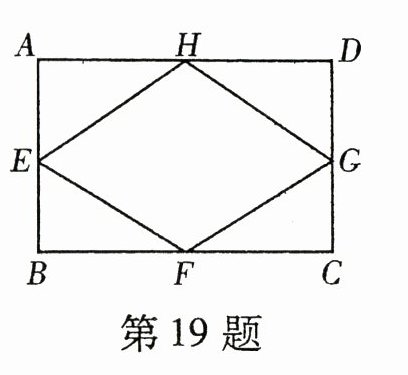
19. 如图所示,在矩形中ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点,若$\tan\angle AEH = \frac{4}{3}$,四边形EFGH的周长为40,则矩形ABCD的面积为_______.

答案:
192
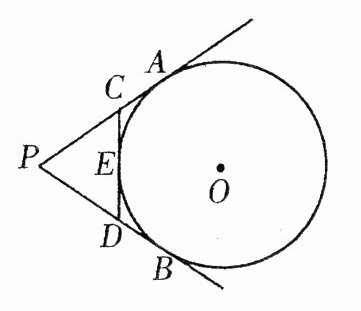
20. 如图所示,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,△PCD的周长等于3r,则$\tan\angle APB$的值是_______.

答案:
$\frac{12}{5}$
21.(8分)计算下列各题:
(1)$\sqrt{2}(2\cos45^{\circ} - \sin60^{\circ}) + \frac{\sqrt{24}}{4}$;
(2)$( - 2)^{0} - 3\tan30^{\circ} - |\sqrt{3} - 2|$.
(1)$\sqrt{2}(2\cos45^{\circ} - \sin60^{\circ}) + \frac{\sqrt{24}}{4}$;
(2)$( - 2)^{0} - 3\tan30^{\circ} - |\sqrt{3} - 2|$.
答案:
解:
(1)$\sqrt{2}(2\cos45^{\circ}-\sin60^{\circ})+\frac{\sqrt{24}}{4}$ $=\sqrt{2}(2\times\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2})+\frac{2\sqrt{6}}{4}$ $=\sqrt{2}(\sqrt{2}-\frac{\sqrt{3}}{2})+\frac{\sqrt{6}}{2}$ $=2-\frac{\sqrt{6}}{2}+\frac{\sqrt{6}}{2}$ $=2$;
(2)$(-2)^{0}-3\tan30^{\circ}-|\sqrt{3}-2|$ $=1 - 3\times\frac{\sqrt{3}}{3}-(2-\sqrt{3})$ $=1-\sqrt{3}-2+\sqrt{3}$ $=-1$
(1)$\sqrt{2}(2\cos45^{\circ}-\sin60^{\circ})+\frac{\sqrt{24}}{4}$ $=\sqrt{2}(2\times\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2})+\frac{2\sqrt{6}}{4}$ $=\sqrt{2}(\sqrt{2}-\frac{\sqrt{3}}{2})+\frac{\sqrt{6}}{2}$ $=2-\frac{\sqrt{6}}{2}+\frac{\sqrt{6}}{2}$ $=2$;
(2)$(-2)^{0}-3\tan30^{\circ}-|\sqrt{3}-2|$ $=1 - 3\times\frac{\sqrt{3}}{3}-(2-\sqrt{3})$ $=1-\sqrt{3}-2+\sqrt{3}$ $=-1$
查看更多完整答案,请扫码查看


