《2025年全练单元卷九年级数学下册人教版》

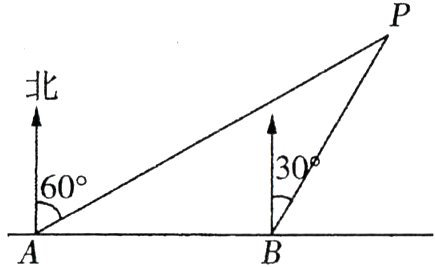
23. (6分)如图，小明同学在东西走向的环海路$A$处，测得海中灯塔$P$在它的北偏东$60^{\circ}$方向上，在$A$的正东400米的$B$处，测得海中灯塔$P$在它的北偏东$30^{\circ}$方向上. 求灯塔$P$到环海路的距离. ($\sqrt{3}$取1.732，结果精确到1米)
　　　

答案：
解：过点$P$作$PC\perp AB$交$AB$的延长线于点$C$，

由题意得，$\angle PAC = 30^{\circ},\angle PBC = 60^{\circ}$，$\therefore \angle APB=\angle PBC - \angle PAC = 30^{\circ}$，$\therefore \angle PAC=\angle APB$，$\therefore PB = AB = 400$米. 在$Rt\triangle PBC$中，$\angle PCB = 90^{\circ},\angle PBC = 60^{\circ},PB = 400$米，$\therefore PC = PB\cdot\sin\angle PBC = 400×\frac{\sqrt{3}}{2}=200\sqrt{3}\approx346.4\approx346$（米）.

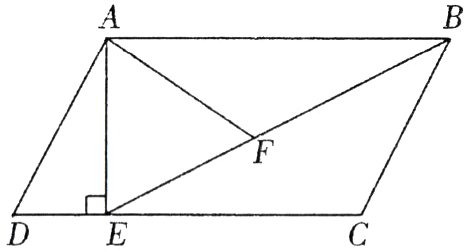
24. (8分)如图，在$\square ABCD$中过点$A$作$AE\perp DC$，垂足为$E$，连接$BE$，$F$为$BE$上一点，且$\angle AFE = \angle D$.
(1)求证：$\triangle ABF\sim\triangle BEC$；
(2)若$AD = 5$，$AB = 8$，$\sin D = \frac{4}{5}$，求$AF$的长.
　　　

答案：
(1)证明：$\because$四边形$ABCD$是平行四边形，$\therefore AB// CD,AD// BC$，$\therefore \angle D+\angle C = 180^{\circ},\angle ABF=\angle BEC$，$\because \angle AFB+\angle AFE = 180^{\circ},\angle AFE=\angle D$，$\therefore \angle C=\angle AFB,\therefore \triangle ABF\sim\triangle BEC$；
(2)解：$\because AE\perp DC,AB// DC$，$\therefore \angle AED=\angle BAE = 90^{\circ}$，在$Rt\triangle ABE$中，根据勾股定理得$BE=\sqrt{AE^{2}+AB^{2}}=\sqrt{4^{2}+8^{2}} = 4\sqrt{5}$，在$Rt\triangle ADE$中，$AE = AD\cdot\sin D = 5×\frac{4}{5}=4$，$\because BC = AD = 5$，由
(1)得$\triangle ABF\sim\triangle BEC$，$\therefore \frac{AF}{BC}=\frac{AB}{BE}$，即$\frac{AF}{5}=\frac{8}{4\sqrt{5}}$，解得$AF = 2\sqrt{5}$.