《2025年全练单元卷九年级数学下册人教版》

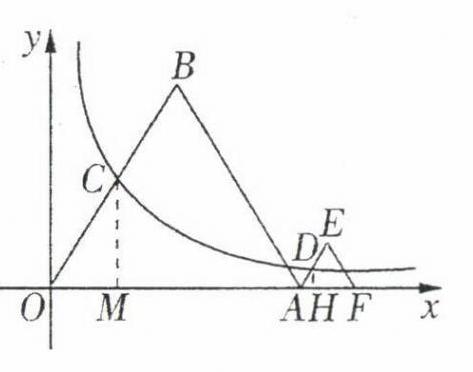
24. (8分)如图，等边$\triangle OAB$和等边$\triangle AFE$的一边都在$x$轴上，反比例函数$y=\frac{k}{x}(x＞0)$经过边$OB$的中点$C$和$AE$中点$D$，已知等边$\triangle OAB$的边长为8.
(1)求反比例函数的解析式；
(2)求等边$\triangle AFE$的周长.

答案：
解：
(1)过$C$作$CM\perp OA$，
$\because \triangle OAB$为边长为$8$的等边三角形，$C$为$OB$中点，
$\therefore OC = 4$，$\angle BOA = 60^{\circ}$，
$\therefore \angle OCM = 30^{\circ}$，
$\therefore OM=\frac{1}{2}OC = 2$，
由勾股定理得$CM = 2\sqrt{3}$，
$\therefore C(2,2\sqrt{3})$，
代入反比例函数的解析式得$k = 4\sqrt{3}$，
则反比例函数的解析式为$y = \frac{4\sqrt{3}}{x}$；
(2)过点$D$作$DH\perp AF$，垂足为点$H$，设$AH = a(a ＞ 0)$.
在$Rt\triangle DAH$中，$\because \angle DAH = 60^{\circ}$，$\therefore \angle ADH = 30^{\circ}$.
$\therefore AD = 2AH = 2a$，
由勾股定理得$DH = \sqrt{3}a$.
$\because$点$D$在第一象限，
$\therefore$点$D$的坐标为$(8 + a,\sqrt{3}a)$.
$\because$点$D$在反比例函数$y = \frac{4\sqrt{3}}{x}$的图象上，
$\therefore$把$x = 8 + a$，$y = \sqrt{3}a$代入反比例函数解析式，
解得$a = 2\sqrt{5}-4$（$a = - 2\sqrt{5}-4 ＜ 0$不符题意，舍去）.
$\therefore AD = 4\sqrt{5}-8$，
$\because$点$D$是$AE$中点，
$\therefore AE = 2AD = 8\sqrt{5}-16$，
$\therefore \triangle AEF$的周长为$24\sqrt{5}-48$.