《2025年全练单元卷九年级数学下册人教版》

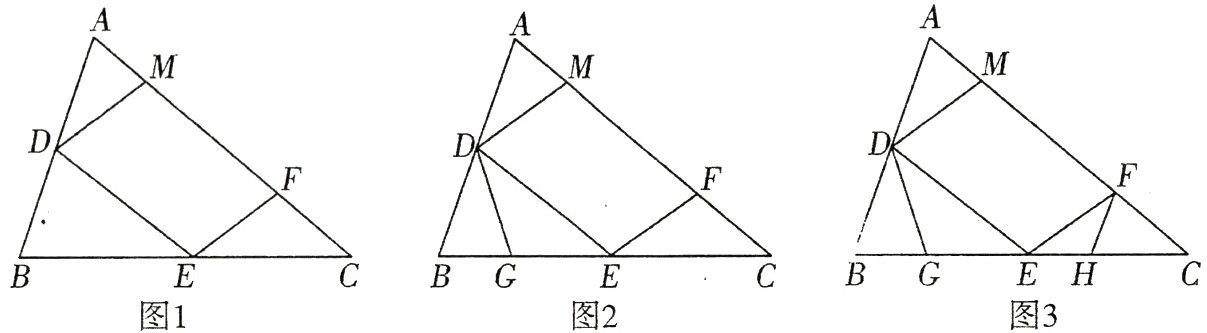
27. (10分)如图1，在锐角△ABC中，D，E分别是AB，BC的中点，点F在AC上，且满足∠AFE = ∠A，DM//EF交AC于点M.
(1)证明：DM = DA；
(2)点G在BE上，且∠BDG = ∠C，如图2，求证：△DEG∽△ECF；
(3)在(2)的条件下，在图3中，取CE上一点H，使得∠CFH = ∠B，若BG = 5，求EH的长.

答案：
(1)证明：
∵ $DM// EF$，
∴ $\angle AMD = \angle AFE$，
∵ $\angle AFE = \angle A$，
∴ $\angle AMD = \angle A$，
∴ $DM = DA$；
(2)解：
∵ $D$，$E$分别是$AB$，$BC$的中点，
∴ $DE// AC$，
∴ $\angle BDE = \angle A$，$\angle DEG = \angle C$，
∵ $\angle AFE = \angle A$，
∴ $\angle BDE = \angle AFE$，
∴ $\angle BDG + \angle GDE = \angle C + \angle FEC$，
∵ $\angle BDG = \angle C$，
∴ $\angle GDE = \angle FEC$，
∴ $\triangle DEG\sim\triangle ECF$；
(3)解：
∵ $\angle BDG = \angle C = \angle DEB$，$\angle B = \angle B$，
∴ $\triangle BDG\sim\triangle BED$，
∴ $\frac{BD}{BE}=\frac{BG}{BD}$，
∴ $BD^2 = BG\cdot BE$，
∵ $\angle AFE = \angle A$，$\angle CFH = \angle B$，
∴ $\angle C = 180^{\circ}-\angle A - \angle B = 180^{\circ}-\angle AFE - \angle CFH = \angle EFH$，
又
∵ $\angle FEH = \angle CEF$，
∴ $\triangle EFH\sim\triangle ECF$，
∴ $\frac{EH}{EF}=\frac{EF}{EC}$，
∴ $EF^2 = EH\cdot EC$，
∵ $DE// AC$，$DM// EF$，
∴ 四边形$DEFM$是平行四边形，
∴ $EF = DM = DA = BD$，
∴ $BG\cdot BE = EH\cdot EC$，
∵ $BE = EC$，
∴ $EH = BG = 5$.