《2025年全练单元卷九年级数学下册人教版》

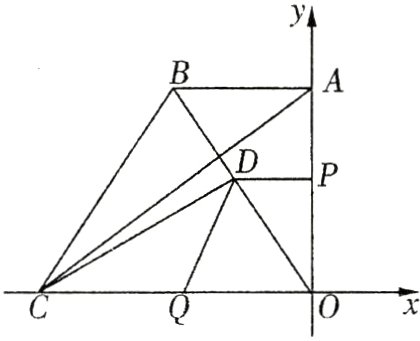
27. (10分)如图，在直角坐标系中，点$A(0,4)$，$B(-3,4)$，$C(-6,0)$，动点$P$从点$A$出发以1个单位/秒的速度在$y$轴上向下运动，动点$Q$同时从点$C$出发以2个单位/秒的速度在$x$轴上向右运动，过点$P$作$PD\perp y$轴，交$OB$于$D$，连接$DQ$. 当点$P$与点$O$重合时，两动点均停止运动. 设运动的时间为$t$秒.
(1)当$t = 1$时，求线段$DP$的长；
(2)连接$CD$，设$\triangle CDQ$的面积为$S$，求$S$关于$t$的函数解析式，并求出$S$的最大值；
(3)运动过程中是否存在某一时刻，使$\triangle ODQ$与$\triangle ABC$相似？若存在，请求出所有满足要求的$t$的值；若不存在，请说明理由.

答案：
解：
(1)由$A(0,4)$，$B(-3,4)$，$C(-6,0)$可知$OA = 4$，$AB = 3$，$CO = 6$，
当$t = 1$时，$AP = 1$，则$OP = 3$，
$\because PD\perp y$轴，$AB\perp y$轴，$\therefore PD// AB$，
$\therefore \frac{DP}{AB}=\frac{OP}{OA}$，$\therefore \frac{DP}{3}=\frac{3}{4}$，$\therefore DP=\frac{9}{4}$；
(2)$\because$时间为$t$秒，动点$P$从点$A$出发以$1$个单位/秒的速度在$y$轴上向下运动，动点$Q$同时从点$C$出发以$2$个单位/秒的速度在$x$轴上向右运动，
$\therefore CQ = 2t$，$AP = t$，$OP = 4 - t$，
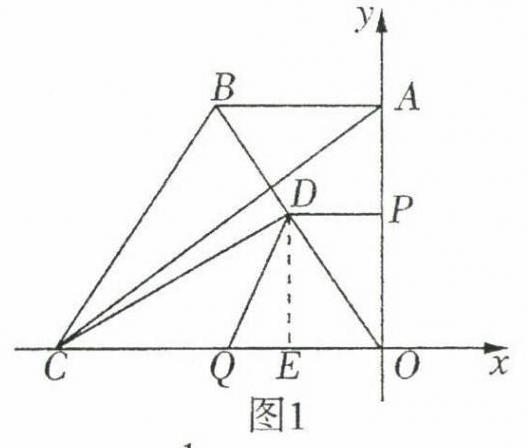
作$DE\perp CO$于点$E$，如图1，
则$DE = OP = 4 - t$，
$\therefore S=\frac{1}{2}\times CQ\times DE=\frac{1}{2}\times2t\times(4 - t)=-t^{2}+4t=-(t - 2)^{2}+4$，
当$t = 2$时，$S_{最大值}=4$；
(3)分两种情况讨论：
①当$0\leq t ＜ 3$时，点$Q$在$CO$上运动（当$t = 3$时，$\triangle ODQ$不存在），
$\because AB// CO$，
$\therefore \angle BOC = \angle ABO ＜ \angle ABC$，
易证得$BO = BC = 5$，
$\therefore \angle BOC = \angle BCO ＞ \angle BCA$，
$\because AB// CO$，
$\therefore \angle BAC = \angle ACO ＜ \angle BCO = \angle BOC$，
$\therefore$当$0\leq t\leq3$时，$\triangle ODQ$与$\triangle ABC$不可能相似；
②当$3 ＜ t\leq4$时，点$Q$在$x$轴正半轴上运动，
延长$AB$交$QD$延长线于点$F$，如图2，
$\because AB// CO$，
$\therefore \angle FBC = \angle BCO = \angle BOC$，
$\therefore \angle ABC = \angle DOQ$，易知$OQ = 2t - 6$，
由$DP// AB$可得$\frac{OD}{OB}=\frac{OP}{OA}$，
$\therefore \frac{OD}{5}=\frac{4 - t}{4}$，$\therefore OD=\frac{20 - 5t}{4}$，
当$\frac{OD}{BC}=\frac{OQ}{BA}$时，$\frac{\frac{20 - 5t}{4}}{5}=\frac{2t - 6}{3}$，$t=\frac{36}{11}$；
当$\frac{OD}{BA}=\frac{OQ}{BC}$时，$\frac{\frac{20 - 5t}{4}}{3}=\frac{2t - 6}{5}$，$t=\frac{172}{49}$；
$\therefore$存在$t=\frac{36}{11}$和$t=\frac{172}{49}$，使$\triangle ODQ$与$\triangle ABC$相似.