《2025年高考必刷小题高中物理人教版》

12. [河南安阳2025届阶段考]一种夜间新型小风扇自带照明装置,简化电路如图所示,电源的电动势为12 V,小灯泡标有“10 V 5 W”的字样,电动机线圈的电阻为0.6 Ω,电流表为理想电表. 闭合开关S后,小灯泡正常发光,电流表的示数为2 A,求：

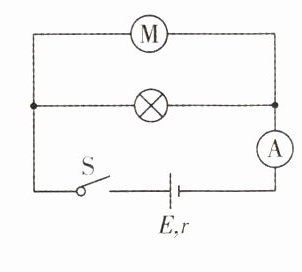
(1)电源的内阻r和电源的输出功率P;
(2)电动机的输出功率和电动机的工作效率.

答案：
(1)1Ω 20W
(2)13.65W 91% **考查点**：含有电动机电路综合计算 【解析】
(1)小灯泡正常发光，可知路端电压$U_{外}=10V$，电源内阻分压$U_{内}=E - U_{外}=2V$，干路中的电流大小$I = 2A$，则电源的内阻$r=\frac{U_{内}}{I}=1Ω$，电源的输出功率$P = U_{外}I = 20W$。
(2)根据$P_{灯}=U_{灯}I_{灯}$可得流过小灯泡的电流大小$I_{灯}=0.5A$，则流过电动机的电流大小$I_M = I - I_{灯}=1.5A$，电动机的输出功率$P_{出}=U_{外}I_M - I_M^2R_M = 13.65W$，电动机的工作效率$\eta=\frac{P_{出}}{U_{外}I_M}\times100\% = 91\%$。

13. [重庆一中2025届阶段考]如图(a)所示,M、N为极板,PQ为足够长的荧光屏,M极板上O₁处有一粒子源,t = 0时刻开始连续释放初速度为零、比荷为$\frac{q}{m}$的带正电的粒子,粒子经过M、N间的加速电场后,从N极板上的细缝O₂进入N和PQ之间的偏转电场. 已知M、N间的电压Uₘₙ - t图像如图(b)所示,O₁O₂连线的延长线与PQ交于O₃,O₂O₃间距离为L,不计粒子在M、N间的加速时间,不计粒子重力和粒子间相互作用,求：

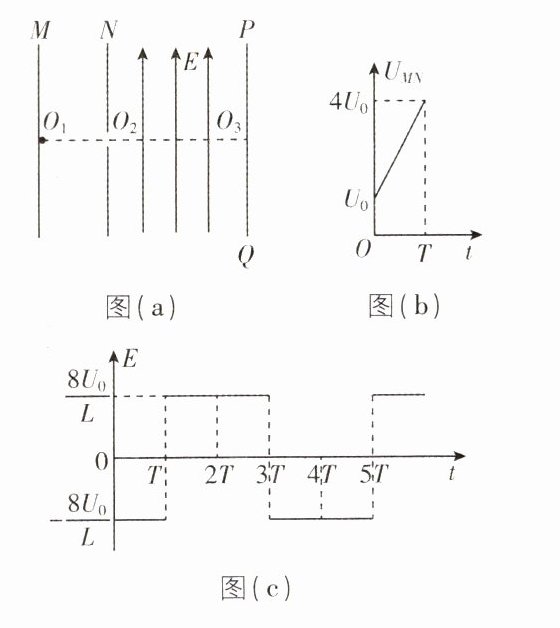
(1)粒子到达细缝O₂时速度v的大小范围;
(2)若N极板和PQ间的偏转电场方向平行PQ向上,场强大小E = $\frac{8U_{0}}{L}$,粒子打到PQ上形成的亮线长度Δy;
(3)若N和PQ间的偏转电场为图(c)所示的周期性变化电场,取平行PQ向下为正方向,从t = 0时刻释放的粒子恰好打到O₃,则t = T时刻释放的粒子打到PQ上的位置.

答案：
(1)$\sqrt{\frac{2qU_0}{m}}\leq v\leq2\sqrt{\frac{2qU_0}{m}}$
(2)$\frac{3}{2}L$
(3)$\frac{L}{2n}(n = 1,2,3\cdots)$ **考查点**：带电粒子在匀强电场和周期性变化的电场中的运动 【解析】
(1)粒子经过M、N间的加速电场过程，根据动能定理$qU_{MN}=\frac{1}{2}mv^2$，解得$v=\sqrt{\frac{2qU_{MN}}{m}}$，所以，M、N间的加速电场场强越大，粒子达到的速度越大，即当$U_{MN}=U_0$时，粒子的速度最小，当$U_{MN}=4U_0$时，粒子的速度最大，即$\sqrt{\frac{2qU_0}{m}}\leq v\leq2\sqrt{\frac{2qU_0}{m}}$。
(2)粒子进入偏转电场后做类平抛运动，根据牛顿第二定律则有$a=\frac{qE}{m}$，水平方向有$L = vt$，竖直方向有$y=\frac{1}{2}at^2$，将速度的两个极值代入可解得$y_1=\frac{L}{2}$，$y_2 = 2L$，粒子打到PQ上形成的亮线长度$\Delta y=y_2 - y_1=\frac{3}{2}L$。
(3)从$t = 0$时刻释放的粒子恰好打到$O_3$，根据竖直方向的运动规律可知，粒子在$0\sim T$向上加速，$T\sim2T$向上减速，$2T\sim3T$向下加速，$3T\sim4T$向下减速，刚好经历一个周期所用时间为$t = 4T$打到$O_3$处，或经历n个周期，即所用时间为$t = 4nT(n = 1,2,3\cdots)$直至打到$O_3$处，则根据速度关系可知$t = T$时刻释放的粒子对应经历$n = 1$个周期则加速时间为$2T$打到PQ上；或者经历$n = 2$个周期则加速时间$2T$又减速时间$2T$打到PQ上……即粒子打到PQ上的距离与周期n有关，由于加速与减速阶段运动满足对称性，根据类平抛运动的规律有$L = v_Tt = 2\sqrt{\frac{2qU_0}{m}}\times\frac{4nT}{2}(n = 1,2,3\cdots)$，$y=n\frac{1}{2}a(2T)^2(n = 1,2,3\cdots)$，解得$y=\frac{L}{2n}(n = 1,2,3\cdots)$。