《2025年通城学典课时作业本七年级数学下册人教版》

14. 根据等式和不等式的性质，我们可以得到比较两数大小的方法：
（1）若$a - b＞0$，则$a$_______$b$；
（2）若$a - b = 0$，则$a$_______$b$；
（3）若$a - b＜0$，则$a$_______$b$；
（4）这种比较大小的方法称为“作差法”，请运用这种方法解决下面的问题：比较$4 + 3a^{2}-2b + b^{2}$与$3a^{2}-2b + 1$的大小。

答案：
(1)＞　
(2)=　
(3)＜　
(4)
∵4+3a²−2b+b²−(3a²−2b+1)=b²+3＞0,
∴4+3a²−2b+b²＞3a²−2b+1

15. 已知关于$x$的不等式$(1 - a)x＞2$的两边都除以$1 - a$，得$x＜\frac{2}{1 - a}$，试化简：$\vert a - 1\vert+\vert a + 2\vert$。

答案： 由题意，得1−a＜0,解得a＞1.
∴|a−1|+|a+2|=a−1+a+2=2a+1

1. （2024·湖北）不等式$x + 1\geq2$的解集在数轴上表示正确的是 （ ）

答案： A

2. 关于$x$的不等式$-2x + a\geq2$的解集如图所示，则$a$的值是 （ ）

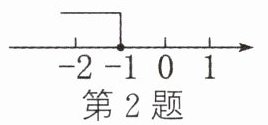
A. 0 B. 2 C. -2 D. 4

答案： A

3. 用不等式表示下面的不等关系：
（1）$x$的$\frac{1}{3}$不大于$-2$：___________；
（2）$m$的4倍不小于$m$与3的差：________。

答案：
(1)$\frac{x}{3}$≤−2　
(2)4m≥m−3

4. （1）不等式$2x + 1＞0$的解集是________；
（2）不等式$2m - 1\leq6$的正整数解是___________。

答案：
(1)x＞$\frac{1}{2}$　
(2)1,2,3

5. （教材P126例3变式）利用不等式的性质解下列不等式：
（1）$2x - 5＜-13$； （2）$-\frac{2}{3}x＞\frac{1}{2}$；
（3）$-9 + 2x\geq5x$； （4）$y + 16\leq9y$。

答案：
(1)x＜−4　
(2)x＜−$\frac{3}{4}$　
(3)x≤−3　
(4)y≥2

12. （教材P128练习第2题变式）利用不等式的性质解下列不等式，并在数轴上表示解集：
（1）$4x - 3\leq5$；
（2）$\frac{5}{6}x＞20$；
（3）$3x\geq8x + 25$；
（4）$\frac{1}{2}y - 1＞7-\frac{5}{2}y$。

答案：

(1)x ≤ 2，解集在数轴上表示如图①所示
(2)x ＞ 24，解集在数轴上表示如图②所示
(3)x ≤ -5，解集在数轴上表示如图③所示
(4)y ＞ $\frac{8}{3}$，解集在数轴上表示如图④所示

13. 当$k$取何值时，方程$2(2x - 1)=1 - 2x$的解不小于关于$x$的方程$8 - k = 2(x + 4)$的解？

答案： 由2(2x−1)=1−2x,得x=$\frac{1}{2}$.由8−k=2(x+4),得x=−$\frac{k}{2}$.由题意，得$\frac{1}{2}$≥−$\frac{k}{2}$,解得k≥−1

14. （教材P127例4变式）某长方体容器长5 cm，宽4 cm，高12 cm. 容器内原有水的高度为2 cm，现准备继续往里面注水，新注入水的体积为$V\ cm^{3}$，求$V$的最大值。

答案： 由于新注入水的体积与原有水的体积的和不能超过容器的容积,即V+4×5×2≤4×5×12,
∴V≤200.
∴V的最大值为200

15. 某水产品市场管理部门规划建造面积为$2400\ m^{2}$的集贸大棚。大棚内设A种类型和B种类型的店面共80间，每间A种类型店面的平均面积为$28\ m^{2}$，每间B种类型店面的平均面积为$20\ m^{2}$，全部店面的建造面积不能超过大棚总面积的85％，那么A种类型的店面最多能设多少间？

答案： 设A种类型的店面有x间，则B种类型的店面有(80−x)间.由题意，得28x+20(80−x)≤2400×85%,解得x≤55.答:A种类型的店面最多能设55间