第55页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
9. 若 MN//x 轴,点 M 的坐标是(-3,5),线段 MN 的长为 6,则点 N 的坐标是__________.
答案:
(-9,5)或(3,5)
10.(教材 P70 习题 9.1 第 5 题变式)如图,请在象棋棋盘上建立平面直角坐标系,使“帅”所在点的坐标为(-1,-2),则“马”所在点的坐标为________.
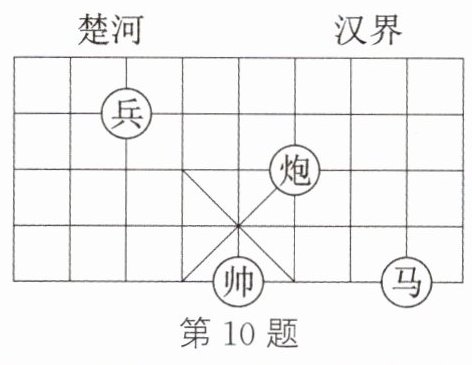

答案:
(2, -2)
11.(教材 P70 习题 9.1 第 9 题变式)已知点 A(-5,0),B(3,0),在 y 轴上有一点 C 满足三角形 ABC 的面积为 16,那么点 C 的坐标为____________.
答案:
(0,4)或(0, -4)
12. 如图,建立平面直角坐标系,使点 B,C 的坐标分别为(0,0)和(3,0),写出点 A,D,E,F,G 的坐标,并指出它们所在的象限.
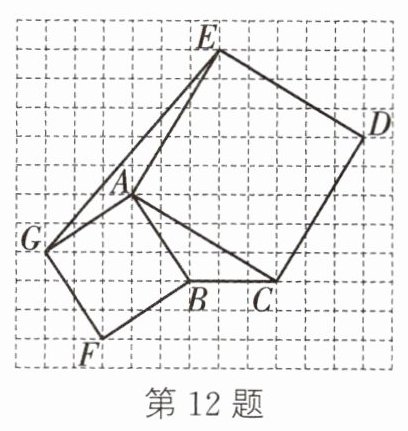

答案:
建立平面直角坐标系如图所示,点A(-2,3)在第二象限,点D(6,5)在第一象限,点E(1,8)在第一象限,点G(-5,1)在第二象限,点F(-3, -2)在第三象限

建立平面直角坐标系如图所示,点A(-2,3)在第二象限,点D(6,5)在第一象限,点E(1,8)在第一象限,点G(-5,1)在第二象限,点F(-3, -2)在第三象限

13. 小超设计的广告模板草图如图所示,小超想通过电话向小强描述该草图. 假如你是小超,你如何利用刚学的平面直角坐标系知识把这个草图告诉小强呢?
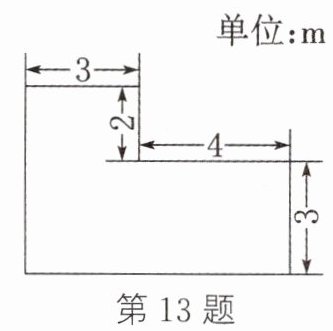

答案:
如图,建立平面直角坐标系(1个单位长度表示1 m),标出点(0,0),(0,5),(3,5),(3,3),(7,3),(7,0),再把各点依次连接,所得图案即为小超设计的草图(答案不唯一)

如图,建立平面直角坐标系(1个单位长度表示1 m),标出点(0,0),(0,5),(3,5),(3,3),(7,3),(7,0),再把各点依次连接,所得图案即为小超设计的草图(答案不唯一)

14. 如图,在平面直角坐标系中,点 A(a,0),B(b,0),且 a,b 满足$\sqrt{a + 1}+(b - 3)^2 = 0$.
(1)a =________,b =________;
(2)若在第三象限内有一点 M(-2,m),用含 m 的式子表示三角形 ABM 的面积;
(3)在(2)的条件下,线段 BM 与 y 轴相交于点 C(0,-$\frac{9}{10}$),当 m =-$\frac{3}{2}$时,P 是 y 轴上的动点,当满足三角形 PBM 的面积是三角形 ABM 的面积的 2 倍时,求点 P 的坐标.
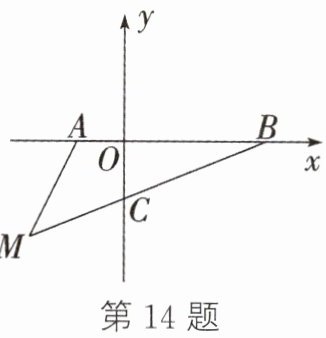
(1)a =________,b =________;
(2)若在第三象限内有一点 M(-2,m),用含 m 的式子表示三角形 ABM 的面积;
(3)在(2)的条件下,线段 BM 与 y 轴相交于点 C(0,-$\frac{9}{10}$),当 m =-$\frac{3}{2}$时,P 是 y 轴上的动点,当满足三角形 PBM 的面积是三角形 ABM 的面积的 2 倍时,求点 P 的坐标.

答案:
(1) -1 3
(2)
∵a = -1,b = 3,
∴A(-1,0),B(3,0)。
∴AB = 4。
∵M(-2,m),且点M在第三象限,
∴m < 0。
∴三角形ABM的面积 = $\frac{1}{2}$×4×(-m) = -2m
(3) 当m = -$\frac{3}{2}$时,M(-2, -$\frac{3}{2}$),S_{三角形ABM} = -2m = -2×(-$\frac{3}{2}$) = 3。
∵三角形PBM的面积是三角形ABM的面积的2倍 = 6,三角形PBM的面积 = 三角形MPC的面积 + 三角形BPC的面积,
∴$\frac{1}{2}$PC×2 + $\frac{1}{2}$PC×3 = 6,解得PC = $\frac{12}{5}$。当点P在点C的下方时,P(0, -$\frac{9}{10}$ - $\frac{12}{5}$),即P(0, -$\frac{33}{10}$);当点P在点C的上方时,P(0, -$\frac{9}{10}$ + $\frac{12}{5}$),即P(0, $\frac{3}{2}$)。综上所述,点P的坐标为(0, -$\frac{33}{10}$)或(0, $\frac{3}{2}$)
(1) -1 3
(2)
∵a = -1,b = 3,
∴A(-1,0),B(3,0)。
∴AB = 4。
∵M(-2,m),且点M在第三象限,
∴m < 0。
∴三角形ABM的面积 = $\frac{1}{2}$×4×(-m) = -2m
(3) 当m = -$\frac{3}{2}$时,M(-2, -$\frac{3}{2}$),S_{三角形ABM} = -2m = -2×(-$\frac{3}{2}$) = 3。
∵三角形PBM的面积是三角形ABM的面积的2倍 = 6,三角形PBM的面积 = 三角形MPC的面积 + 三角形BPC的面积,
∴$\frac{1}{2}$PC×2 + $\frac{1}{2}$PC×3 = 6,解得PC = $\frac{12}{5}$。当点P在点C的下方时,P(0, -$\frac{9}{10}$ - $\frac{12}{5}$),即P(0, -$\frac{33}{10}$);当点P在点C的上方时,P(0, -$\frac{9}{10}$ + $\frac{12}{5}$),即P(0, $\frac{3}{2}$)。综上所述,点P的坐标为(0, -$\frac{33}{10}$)或(0, $\frac{3}{2}$)
查看更多完整答案,请扫码查看


